跳跃表

发表于 分类于 阅读次数：

1. 概述

跳跃表是一种数据结构。它允许快速查询一个有序连续元素的数据链表。跳跃表的平均查找和插入时间复杂度都是O(logn)，优于普通队列的O(n)。快速查询是通过维护一个多层次的链表，且每一层链表中的元素是前一层链表元素的子集。一开始时，算法在最稀疏的层次进行搜索，直至需要查找的元素在该层两个相邻的元素中间。这时，算法将跳转到下一个层次，重复刚才的搜索，直到找到需要查找的元素为止，跳跃表示意图如下所示。
skip-list
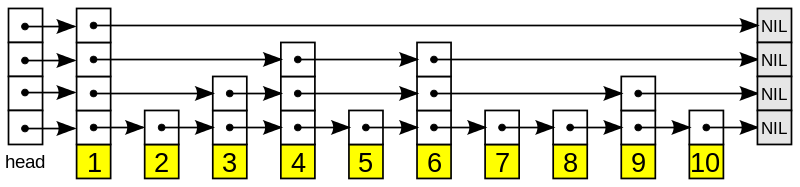从图中可以看到， 跳跃表主要由以下部分构成：

  • 表头（head）：负责维护跳跃表的节点指针；
  • 跳跃表节点：保存着元素值，以及多个层。
  • 层：保存着指向其他元素的指针，高层的指针越过的元素数量大于等于低层的指针，为了提高查找的效率，程序总是从高层先开始访问，然后随着元素值范围的缩小，慢慢降低层次。
  • 表尾：全部由 NULL 组成，表示跳跃表的末尾。

本篇文章将以redis中的跳跃表为例进行介绍，代码用java进行了重写，为方便看懂，简化了部分流程。

2. 层数

跳跃表是按照层构建的，每一层都是一个有序链表，最底层包含了所有的元素，每一个更高层都包含了指向下层的指针，也可以说高层是下层数据的“索引”。通过对高层数据的检索可以实现类似二分查找的效果，但是要准确判断出数据是否出现在高层通且对之前数据的层次进行调整是一个复杂的过程，要实现的算法可以参考AVL树和红黑树。在跳跃表中，通过概率的方式，近似得出数据的层数，简化操作。

每个更高层都充当下面列表的“快速通道”，在第i层中的元素按某个固定的概率p（通常为1/2或1/4出现在第i+1层），以Redis中的跳跃表为例：

level 1的概率为 0.75
level 2的概率为 0.75 * 0.25
level 3的概率为 0.75 * 0.25 * 0.25
…
level 31的概率为 0.75 * 0.25^30
level 32的概率为 0.75 * 0.25^31

代码如下所示：

1
2
3
4
5
6
7
8
9
private int zslRandomLevel() {
    int level = 1;

    while ((random.nextInt() & 0xFFFF) < (ZSKIPLIST_P * 0xFFFF)) {
        level += 1;
    }

    return (level < ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

其中ZSKIPLIST_MAXLEVEL为32，ZSKIPLIST_P为0.25（即1/4）,random.nextInt() & 0xFFFF为16位整数，ZSKIPLIST_P * 0xFFFF为16位整数的1/4。从概率学的角度来说，大于ZSKIPLIST_P * 0xFFFF的概率为3/4，即level 1的概率是0.75，level 2，概率是0.75 * 0.25，后面的层次依次类推。

在介绍跳跃表的插入和删除之前，先看下跳跃表的数据结构（参考redis的实现进行了简化）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
public class ZSkipList<T extends Comparable<? super T>> {

    // 最大层数
    private static final int ZSKIPLIST_MAXLEVEL = 32;

    // P，概率
    private static final double ZSKIPLIST_P = 0.25;

    // 头结点
    private ZSkipListNode<T> header;

    // 节点总数
    private int length;

    // 层数
    private int level;

    // 随机数
    private Random random;
	
	public ZSkipList() {

        this.length = 0;
        this.level = 1;

        ZSkipListNode<T> nullNode = new ZSkipListNode<>();
        this.header = new ZSkipListNode<>(null, ZSKIPLIST_MAXLEVEL);

        random = new Random();
    }
	
    /**
     *  结点
     * @param <T>
     */
    private static class ZSkipListNode<T extends Comparable<? super T>> {
        // 键值
        T key;

        // 层次
        ZSkipListLevel<T>[] levels;

        public ZSkipListNode() {
        }

        public ZSkipListNode(T key, int level) {
            this.key = key;
            this.levels = new ZSkipListLevel[level];

            ZSkipListLevel<T> listLevel = null;

            for (int i = 0 ; i < level ; i++) {
                listLevel = new ZSkipListLevel<>();
                this.levels[i] = listLevel;
            }

        }

    }

    /**
     *  层
     * @param <T>
     */
    private static class ZSkipListLevel<T extends Comparable<? super T>> {

        // 下一个结点
        ZSkipListNode<T> next;

        // 跨度，当前结点与后继结点蹭相隔几个结点
        int span;

        public ZSkipListLevel() {
            this.next = null;
            this.span = 0;
        }
    }
	
	...
}

3. 插入

插入操作的步骤：

  • 1）找出插入结点每一层的前驱结点及排名；
  • 2）随机生成插入结点的层数；
  • 3）在每一层链表中插入结点，修改结点跨度；
  • 4）更新结点数。

代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
/**
 * 向跳跃表中插入结点
 * @param key 插入元素
 */
public void insert(T key) {

    Preconditions.checkNotNull(key);

    // update存放插入结点每一层的前驱结点，
    ZSkipListNode<T>[] update = new ZSkipListNode[ZSKIPLIST_MAXLEVEL];

    // rank存放结点在每一层上的排名
    int [] rank = new int[ZSKIPLIST_MAXLEVEL];

    // 用于遍历插入结点的位置
    ZSkipListNode<T> creeper = header;

    /*
    *   1、找到每一个层次的前驱结点及每一个层次的排名。
     *  从最顶层开始遍历,从上往下查的插入结点的位置,如果在该层中结点大于插入结点的值,
     *  则移向该结点的下一层开始查找,同时记录插入结点的排名,用于计算插入结点与前一个
     *  结点之间的跨度(span).
     */
    for (int i = level - 1; i >= 0; i--) {

        // 用于插入结点在某一个层次的排名,在最高层排名默认值为0;
        // 非最高层默认值上一个层次的值,会在下面的循环中依次增加排名.
        rank[i] = i == level-1 ? 0 : rank[i+1];

        // 如果当前结点小于等于插入结点,则继续查找.
        while (creeper.levels[i].next != null && key.compareTo(creeper.levels[i].next.key) > 0) {

            // 排名数加上当前结点到一个结点之间的跨度
            rank[i] += creeper.levels[i].span;

            // 指向后继结点
            creeper = creeper.levels[i].next;
        }

        // 找到当前层次中后继结点大于等于插入结点的结点,作为插入结点的前驱结点
        update[i] = creeper;
    }

    // 2、随机生成插入结点的层次
    // 用冥次定律,生成一个随机的层次
    int newLevel = zslRandomLevel();

    // 如果生成的层次大于当前跳跃表的最大层次,则初始化大于的层次.
    if (newLevel > level) {
        for (int i = level ; i < newLevel ; i++) {
            rank[i] = 0;
            update[i] = header;
            update[i].levels[i].span = this.length;
        }
        this.level = newLevel;
    }

    //System.out.println("newLevel = " + newLevel + " ; key=" + key);

    // 新建插入的结点
    ZSkipListNode<T> node = new ZSkipListNode<>(key, level);

    /*
    *  3、插入结点及更新跨度
    *  1）在每一个层次中插入一个结点，该操作就是链表的插入操作，比较简单；
    *  2）更新产驱结点及当前结点的跨度。
    */
    for (int i = 0; i < newLevel; i++) {

        // 3.1 插入结点的后继结点指向前驱结点的后继结点；
        // 3.2 前驱结点的后继结点指向插入结点。
        node.levels[i].next = update[i].levels[i].next;
        update[i].levels[i].next = node;

        /* 插入一个新结点，等于在前驱结点与其后继结点之间插入一个结点，之前的
        *  span等于前驱结点与其后继结点之间的跨度，现在一分为二：前驱结点与插入结点的跨度和
        *  插入结点与后继结点的跨度。前一个值即为前驱结点的跨度，等于上下两个层次排名的差值，
        *  后一个值即为插入结点的跨度，等于前驱结点原先的span减去前一个值。
        */
        node.levels[i].span = update[i].levels[i].span - (rank[0] - rank[i]);
        update[i].levels[i].span = (rank[0] - rank[i]) + 1;
    }

    // 如果插入结点的层次小于当前最大的层数，则更新高层的spsn。
    for (int i = newLevel; i < this.level; i++) {
        update[i].levels[i].span++;
    }

    // 4. 结点数加1.
    this.length++;
}

以插入12, 45, 63, 21, 99, 87, 23, 47, 30, 50数组为例，分析插入结点的流程，图形的格式说明：head[00](01)–>12(00)，定义为head[层数](跨度,当前结点与下一个结点之间相隔结点数)–>下一个结点(跨度)。

  • 1）插入12，层数为1，当前只有一层，12为最底层的第一个结点，头结点到12中间的跨度为1（包括12在内）。

    1
    2
    3
    new node = 12, level = 1

    head[00](01)-->12(00)

  • 2）插入45，层数为2，跳跃表新增一层，在两层中插入45，其中第二层头结点到45结点的跨度为2（包括45在内）。

    1
    2
    3
    4
    new node = 45, level = 2 

    head[01](02)----------->45(00)
    head[00](01)-->12(01)-->45(00)

  • 3）插入63，层数为1，只插入到第一层。

    1
    2
    3
    4
    new node = 63, level = 1 

    head[01](02)----------->45(01)
    head[00](01)-->12(01)-->45(01)-->63(00)

  • 4）插入21，层数为2。

    1
    2
    3
    4
    new node = 21, level = 2 

    head[01](02)----------->21(01)-->45(01)
    head[00](01)-->12(01)-->21(01)-->45(01)-->63(00)

  • 5）插入99，层数为1。

    1
    2
    3
    4
    new node = 99, level = 1 

    head[01](02)----------->21(01)-->45(02)
    head[00](01)-->12(01)-->21(01)-->45(01)-->63(01)-->99(00)

  • 6）插入87，层数为1。

    1
    2
    3
    4
    new node = 87, level = 1 

    head[01](02)----------->21(01)-->45(03)
    head[00](01)-->12(01)-->21(01)-->45(01)-->63(01)-->87(01)-->99(00)

  • 7）插入23，层数为1。

    1
    2
    3
    4
    new node = 23, level = 1 

    head[01](02)----------->21(02)----------->45(03)
    head[00](01)-->12(01)-->21(01)-->23(01)-->45(01)-->63(01)-->87(01)-->99(00)

  • 8）插入47，层数为2。

    1
    2
    3
    4
    new node = 47, level = 2 

    head[01](02)----------->21(02)----------->45(01)-->47(03)
    head[00](01)-->12(01)-->21(01)-->23(01)-->45(01)-->47(01)-->63(01)-->87(01)-->99(00)

  • 9）插入30，层数为1。

    1
    2
    3
    4
    new node = 30, level = 1 

    head[01](02)----------->21(03)-------------------->45(01)-->47(03)
    head[00](01)-->12(01)-->21(01)-->23(01)-->30(01)-->45(01)-->47(01)-->63(01)-->87(01)-->99(00)

  • 10）插入87，层数为4。

    1
    2
    3
    4
    5
    6
    new node = 50, level = 4 

    head[03](07)-------------------------------------------------------->50(03)
    head[02](07)-------------------------------------------------------->50(03)
    head[01](02)----------->21(03)-------------------->45(01)-->47(01)-->50(03)
    head[00](01)-->12(01)-->21(01)-->23(01)-->30(01)-->45(01)-->47(01)-->50(01)-->63(01)-->87(01)-->99(00)

4. 删除

删除操作的步骤为：

  • 1）找出删除结点每一层的前驱结点；
  • 2）将前驱结点的后继结点指向删除指点的后继结点，并修改前驱结点的跨度；
  • 3）删除空的层并对结点数减一。

跳跃表的删除实际就是单向链表的删除，其代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * 删除一个已有结点
 * @param key
 */
public void delete(T key) {

    // 1、找到key对应的结点
    Preconditions.checkNotNull(key);

    ZSkipListNode<T>[] update = new ZSkipListNode[ZSKIPLIST_MAXLEVEL];
    // 获取前驱结点
    predecessorLevels(key, update);

    // 第一层的后继结点有可能是删除的结点(有可能删除一个不存在的结点)
    ZSkipListNode<T> node = update[0].levels[0].next;

    // 判断是否是删除的结点
    if (key.compareTo(node.key) == 0) {
        for (int i = 0; i < this.level; i++) {
            if (update[i].levels[i].next == node) {

                // 前驱结点的跨度等于之前的跨度再加上删除结点的跨度,再减去删除结点.
                update[i].levels[i].span += node.levels[i].span -1;
                update[i].levels[i].next = node.levels[i].next;
            } else {
                update[i].levels[i].span -= 1;
            }
        }

        // 清理空的层
        while (this.level > 1 && this.header.levels[this.level-1].next == null) {
            this.level--;
        }

        // 结点数减一
        this.length--;
    }

}

/**
 * 获取每一层的前驱结点
 * @param key
 * @param update
 */
public void predecessorLevels(T key, ZSkipListNode<T>[] update) {

    ZSkipListNode<T> creeper = header;

    for (int i = level - 1; i >= 0; i--) {

        while (creeper.levels[i].next != null && key.compareTo(creeper.levels[i].next.key) > 0) {
            creeper = creeper.levels[i].next;
        }

        update[i] = creeper;
    }
}

删除实例如下：

1
2
3
4
5
6
7
8
9
10
11
删除前的跳跃表：
head[03](04)----------------------------->30(06)
head[02](04)----------------------------->30(05)-------------------------------------->87(01)
head[01](01)-->12(01)-->21(02)----------->30(05)-------------------------------------->87(01)
head[00](01)-->12(01)-->21(01)-->23(01)-->30(01)-->45(01)-->47(01)-->50(01)-->63(01)-->87(01)-->99(00)

删除30后的跳跃表：
head[02](08)----------------------------------------------------------------->87(01)
head[01](01)-->12(01)-->21(06)----------------------------------------------->87(01)
head[00](01)-->12(01)-->21(01)-->23(01)-->45(01)-->47(01)-->50(01)-->63(01)-->87(01)-->99(00)

在每一层的链表中都会删除30这个结点，同时更新前驱结点的跨度。因为第4层只有30这个结点，删除之后，该层没有结点，就要减少跳跃表的层数。

6. 总结

跳跃表的发明者对其的评价：

跳跃列表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界，并且更简单、更快速和使用更少的空间

跳跃表相对平衡二叉树而言，实现简单，又能在近似O(logn)时间复杂度的情况下实现数据的检索和插入，这或许也是在redis中使用跳跃表代替红黑树的原因之一。

参考：

1. 跳跃列表

2. Redis 源码研究之skiplist

3. redis源码