垃圾回收之回收算法
几乎所有的现代编程语言都使用动态内存分配,即允许进程在运行时分配或释放无法在编译期确定大小的对象,这些对象的存活时间有可能超出创建者的生存周期。动态分配的对象存在于堆(heap)中而不是栈(stack)或者静态区(statically)中。在内存的管理方式上,有两种方式:1)显示内存释放,由开发人员显示的创建或释放对象;2)自动动态内存管理,由编程语言的运行时系统(虚拟机)负责内存的回收。自动动态内存管理可以显著地降低开发成本,提供程序的健壮性。我们这篇文章主要便是讲述内存管理中常用垃圾回收算法,并结合 java 来分析内部的实现。
垃圾回收的目的是回收程序不再使用的对象所占用的空间,任何具备自动内存管理系统的语言都要有三个功能:
- 为新对象分配空间;
- 确定存活对象;
- 回收死亡对象所占用的空间。
内存分配与回收是相关性比较强的两个功能,内存管理系统都要具备这两个功能;在实现中,使用指针的可达性来近似对象的存活:只有当堆中存在一条从根出发的指针链能最终到达某个对象时,才能认定该对象存活,更进一步,如果不存在这一条指针链,则认为对象死亡,其空间可以得到回收。回收死亡对象包括两种方式:1)直接释放该对象,有可能会与前后的空闲对象进行合并;2)将存活对象进行移动或整理,减少内存碎片的问题。
1. 标记 - 清扫
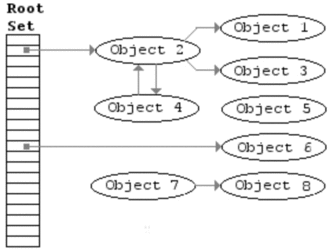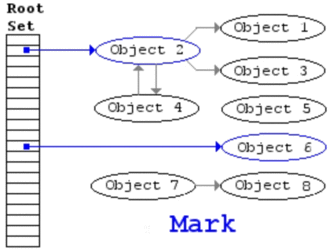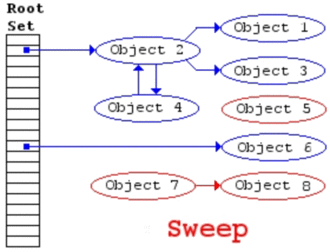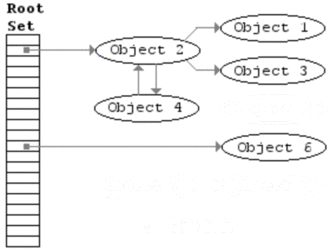
标记 - 清除算法分为两个阶段:1)追踪(trace)阶段,即回收器(回收程序)从根集合(寄存器、线程栈、全局变量)开始遍历对象图,并标记(mark)所遇到的每一个对象;2)清扫(sweep)阶段,即回收器检查堆中每一个对象,并将所有未标记的对象当作垃圾进行回收。其算法如下所示:
1 | New(): // 新建对象 |
在新建对象的方法中,会给对象分配一块内存空间,如果堆中没有足够的可用空间,会进行一次内存回收,回收之后再分配一次内存,如果堆中仍然没有足够的可用空间,则抛出错误。 在回收对象的方法中,会从根集合开始,对存活的对象进行标记,然后遍历整个堆,对未标记的对象执行回收操作。
1 | markFromRoots(): |
说明 1) Roots:表示根集合,包含指针扫描的起点,主要是指寄存器、线程栈和全局变量; 2)Pointers(ref):表示ref指针指向的对象中包含的指针集合;
如何得到根集合和对象中的指针集合,我们会在后面的文章再讲解,现在假定我们已经知道这些值。
我们可以将堆看作是一个图的结构,对象是结点,结点间的指针(引用)是边,根便是图的起始结点。对堆对象进行标记就是对对象图进行遍历操作,在上面的算法中使用的深度优先遍历算法。在算法中使用栈来实现工作列表,先从根结点开始,将标记过的对象放入工作列表中,然后取出对象对其所指向的对象进行标记,直到工作列表为空。
1 | sweep(start,end): |
清除操作将堆中的所有对象看作一个对象列表,可以从堆的起始地址遍历所有对象,如果对象被标记则取消标记,进行下一轮的回收,如果未标记,则说明是一个死对象,则进行回收,回收的策略取决于具体的实现。如何对堆中的对象进行遍历,我们将在后面的文章进行讲解。一个完整的标记-清扫算法如下所示:
1.1 三色遍历
标记的核心操作之一就是从给定的根集合出发去遍历对象图。遍历它有两种典型顺序:深度优先(DFS)和广度优先(BFS)。
广度优先遍历的典型实现思路是三色遍历:给对象赋予白、灰、黑三种颜色以标记其遍历状态:
1)白色:未遍历到的对象,所有对象的初始状态都是白色;
2)灰色:已遍历到但还未处理完的对象,即还有出边没有遍历;
3)黑色:已遍历完的对象,所有出边已经遍历。 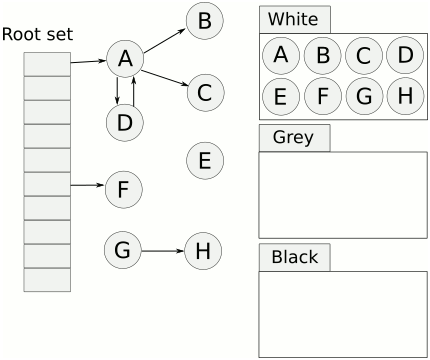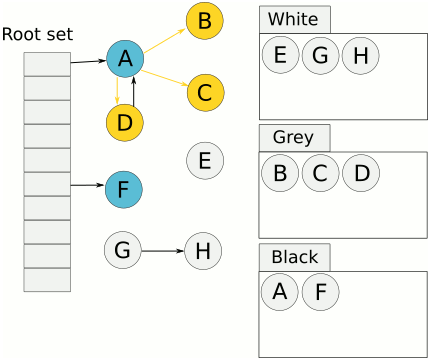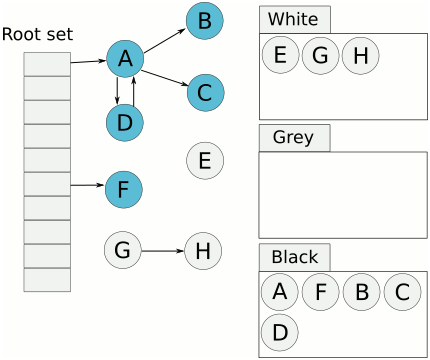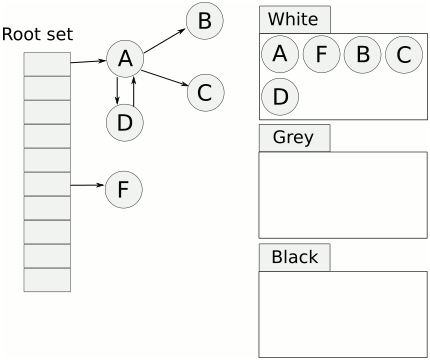
算法的步骤如下: 1)算法开始,所有的对象标记为白色; 2)从根集合开始,将引用到的对象标记为灰色; 3)从灰色集合中取出对象,遍历其所有出边,将遍历到的对象标记为灰色,遍历结束,将该对象标记为黑色; 4)重复第三步,直到没有灰色对象,最后未被遍历到白色对象即为死亡对象。
2. 标记 - 整理
标记-清扫算法只是对不再存活的对象进行释放,不会对存活的对象进行移动,这会造成碎片的问题,即使可用内存大于对象分配所需的内存,由于这些内存不是连续的,最终会导致分配失败。为了解决这个问题,引入了标记-整理算法。该算法在标记-清除算法的基础上,会将存活的对象统一移动到某一端,让它们连续存储在一起,从而得到较大的可用内存。根据移动前后的位置,有三种移动的顺序:
- 任意顺序:对象的移动顺序与它们的原始排列顺序和引用没有关系;
- 线性顺序:将具有关联关系的对象排列在一一起,如对象之间的引用关系或同一个数据结构中相邻的对象;
- 滑动顺序:将对象滑动到堆的一端,保持对象在堆中原有的分配顺序。
这里会分别介绍四种整理算法:1)双指针整理算法;2)Lisp
2算法;3)引线整理算法;4)单次遍历算法。其中除了双指针整理算法是按照任意顺序移动对象,其它算法都是滑动顺序。所有的整理算法都遵循下面的范式:
1
2
3collect():
markFromRoots();
compact()
2.1 双指针整理算法
双指针整理算法需要遍历两次堆,适用于只包含固定大小对象的区域。该算法流程如下:
- 计算出“高水位标记”,地址大于该阈值的存活对象都被移动该阈值之下;
- 设置两个指针,free 指针指向区域始端,scan 指针指向区域末端;
- 第一次遍历,free 指针向后移动,找到空闲区域为止,scan 指针向前移动,找到存活对象为止;
- 将 scan 指针指向的存活对象移动到 free 指向的空闲区域,并将scan对象中的“转发指针”设置为 free ,方便下次做指针的更新;
- 重新移动 free 及 scan 指针,直到 free > scan 为止;
- 第二次遍历,更新指针存活对象中的指针,如果指针指向的地址中存在“转发指针”则直接更新该转发地址,算法结束。
算法过程如下所示: 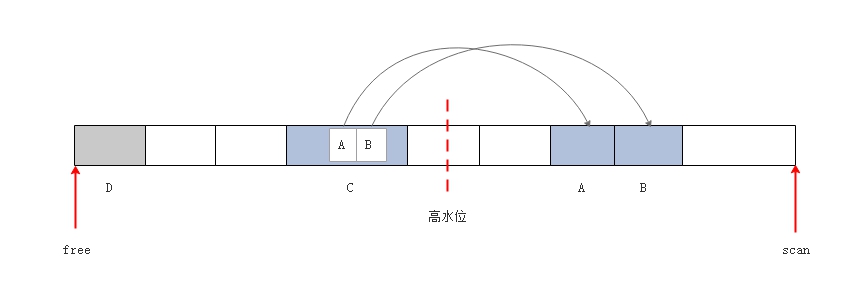 初始状态下:1)有A, B,
C, D 4个存活对象,其中 C 对象中有两个指针分别指向 A 和 B 两个对象。
初始状态下:1)有A, B,
C, D 4个存活对象,其中 C 对象中有两个指针分别指向 A 和 B 两个对象。 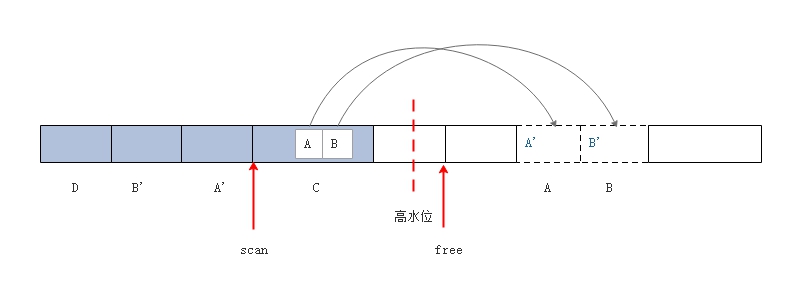 第一次遍历,将 A 和 B
两个对象移动到低地址区域,同时将移动后的地址写入到之前的对象中。
第一次遍历,将 A 和 B
两个对象移动到低地址区域,同时将移动后的地址写入到之前的对象中。 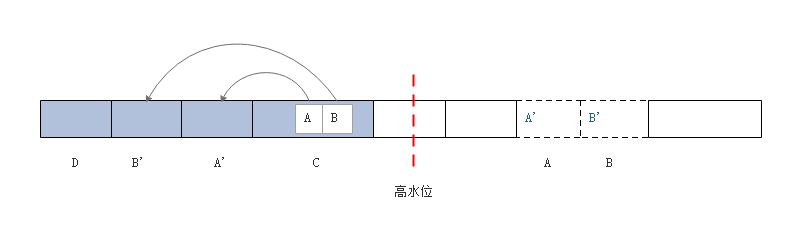 第二次遍历,根据“转移地址”更新 C 对象中的 A
和 B 两个指针。
第二次遍历,根据“转移地址”更新 C 对象中的 A
和 B 两个指针。
在双指针整理算法中,移动前后的存储对象的空闲空间大小最好是相等的,否则寻找匹配大小的空闲空间需要来回移动free指针,这样会降低算法的执行效率,另外,在该算法中,移动的顺序是任意的,会破坏赋值操作的局部性。
整理算法的伪代码如下所示: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37compact():
relocate(HeapStart, HeapEnd)
updateReferences(HeapStart, free)
relocate(start, end):
free = start
scan = end
while free < scan
while isMarked(free)
unsetMarked(free)
free = free + size(free) /* 寻找下一个空闲块 */
while not isMarked(scan) && scan > free
scan = scan - size(scan) /* 寻找前一个存活对象 */
if scan > free
unsetMarked(scan)
move(scan, free)
*scan = free /* 记录转发地址 */
free = free + size(free)
scan = scan - size(scan)
updateReferences(start, end):
for each fld in Roots /* 更新指向被移动对象的根 */
ref = *fld
if ref >= end
*fld = *ref /* 更新转发地址 */
scan = start
while scan < end
for each fld in Pointers(scan)
ref = *fld
if ref >= end
*fld = *ref /* 更新转发地址 */
scan = scan + size(scan) /* 下一个对象 */
2.2 Lisp 2 算法
Lisp 2 算法对管理的对象大小没有限制,它可以管理包含多种大小对象的空间,同时移动的时候采用滑动顺序,不会改变对象的相对顺序。不过整理的过程需要遍历三次堆,算法的流程如下:
- 第一次遍历:计算移动的位置。假定需要整理的内存区域起始地址、结束地址分别为 heapStart 、heapEnd,移动后的内存区域起始地址为toRegion,其中 heapStart 和 toRegion 可以是同一个地址;
- 将 scan 指向 heapStart 地址,free 指针指向 toRegion地址,开始遍历存活对象,找到存活对象之后,将存活对象中的 forwadingAddress 域设置为 free,然后将 scan 和 free 向后移动 size(存活对象) 大小的位置,当 scan 大于 heapEnd 之后,第一次遍历结束;
- 第二次遍历:更新转发地址的值。遍历根集合和堆中所有的对象,更新对象指针域中指向的地址为 forwadingAddress 中的地址;
- 第三次遍历:移动对象。遍历堆中所有对象,将对象移动到 forwadingAddress 指向的地址。
算法过程如下所示: 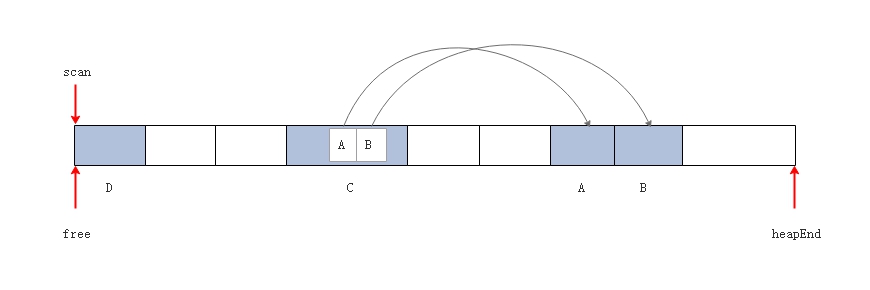 初始状态下:1)有A, B, C, D
4个存活对象,其中 C 对象中有两个指针分别指向 A 和 B 两个对象。
初始状态下:1)有A, B, C, D
4个存活对象,其中 C 对象中有两个指针分别指向 A 和 B 两个对象。 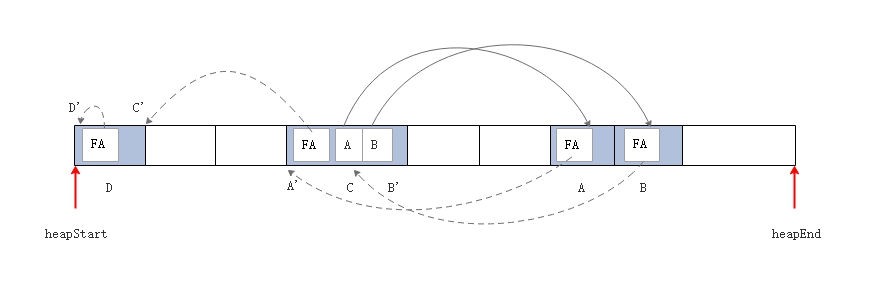 第一次遍历,在每一个对象中,增加一个forwadingAddress 域,即
FA域,存放移动后的地址,移动后的地址通过遍历可以获得。
第一次遍历,在每一个对象中,增加一个forwadingAddress 域,即
FA域,存放移动后的地址,移动后的地址通过遍历可以获得。 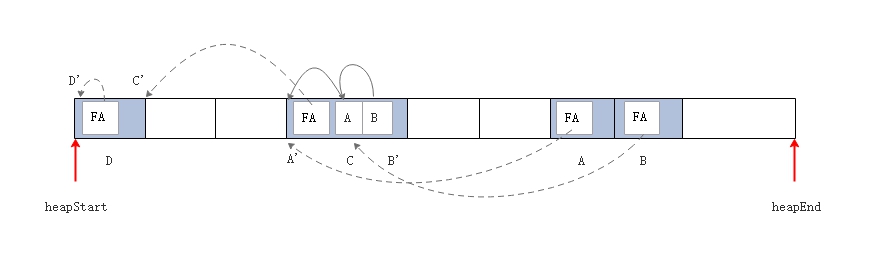 第二次遍历,更新堆中所有对象的指针域,重新指向 FA
域指向的地址。
第二次遍历,更新堆中所有对象的指针域,重新指向 FA
域指向的地址。 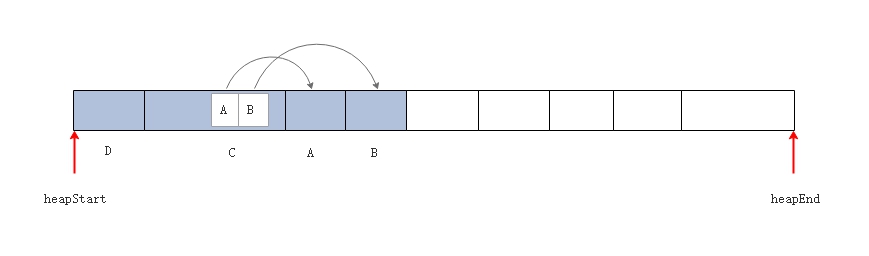 第三次遍历,根据对象中的 FA 域的值,将该对象移动到
FA 域指向的地址。
第三次遍历,根据对象中的 FA 域的值,将该对象移动到
FA 域指向的地址。
Lisp 2 算法需要遍历三次堆,同时对象中需要一个 forwadingAddress 域,用来存放“转发的地址”。
Lisp 2 算法的伪代码如下所示:
1 | compact(): |
2.3 引线整理算法
Lisp 2
算法有两个缺陷:1)需要遍历三次堆;2)每一个对象需要额外的空间来记录转发地址。引线整理算法通过一种不同的策略来解决指针更新的问题,该算法不需要额外存储,且支持滑动整理。引线算法要求对象头部存在足够的空间来保存一个地址,引线的目的是通过对象
N 可以找到所有引用了该对象的对象,实现的方法是临时反转指针的方向。 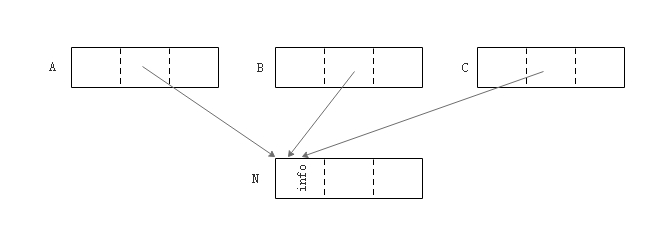 引线之前,三个对象引用了对象N
引线之前,三个对象引用了对象N 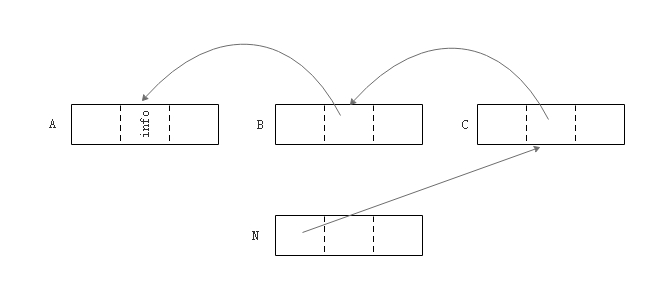 引线之后,所有指向对象 N
的指针都被“引线”,因此可以通过对象 N 找到引用了对象 N 的对象。在对象 N
中,指向下一个对象的指针保存在其头部的某个值中,该头部以前的值被(临时地)移动到对象
A 中引用了对象 N 的指针域中。
引线之后,所有指向对象 N
的指针都被“引线”,因此可以通过对象 N 找到引用了对象 N 的对象。在对象 N
中,指向下一个对象的指针保存在其头部的某个值中,该头部以前的值被(临时地)移动到对象
A 中引用了对象 N 的指针域中。
引线整理算法需要两次堆遍历,第一次遍历实现堆中前向指针(从低地址指向高地址的指针)的引线,第二次遍历实现堆中后向指针(从高地址指向低地址的指针),其算法流程如下:
- 第一次遍历,从对根进行引线,然后在堆中从头到尾进行扫描,同时计算转发地址 free,扫描到对象 N 时,根据前向指针,修改引用对象 N 的所有对象(其地址小于对象 N)的指针,将其设置为 free。同时对对象 N 的所有指针进行引线(包括前向指针和后向指针)。
- 第二次遍历,在堆中从头到尾进行扫描,计算转发地址,扫描到对象 N 时,根据后向指针,修改引用对象 N 的所有对象(其地址大于对象 N)的指针,将其设置为 free,最后将对象移动到 free。
算法过程如下所示: 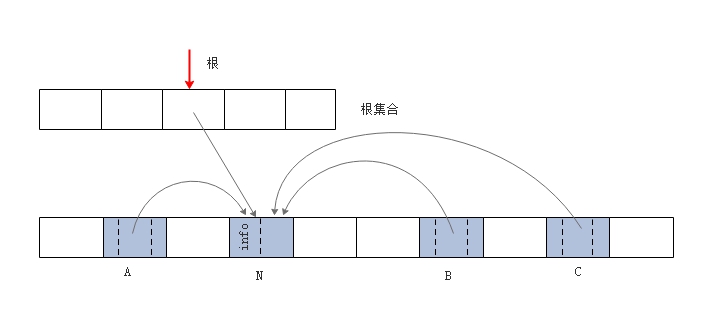 初始状态下,有一个根对象指向对象 N, 三个对象 A, B 及 C 指向 对象 N 。
初始状态下,有一个根对象指向对象 N, 三个对象 A, B 及 C 指向 对象 N 。
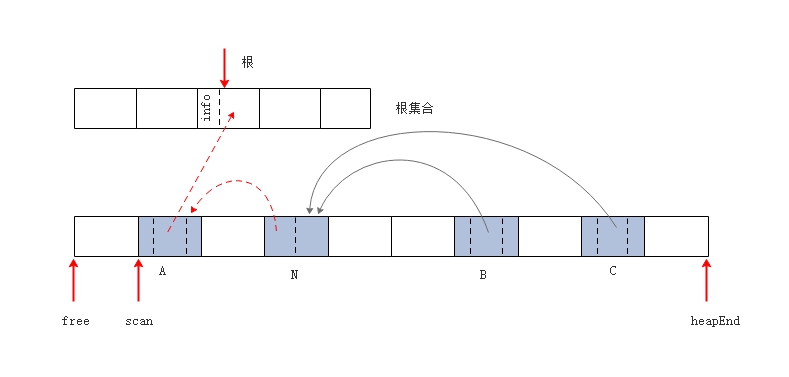 第一次遍历,扫描到对象
A,实现了前向指针的引线。
第一次遍历,扫描到对象
A,实现了前向指针的引线。 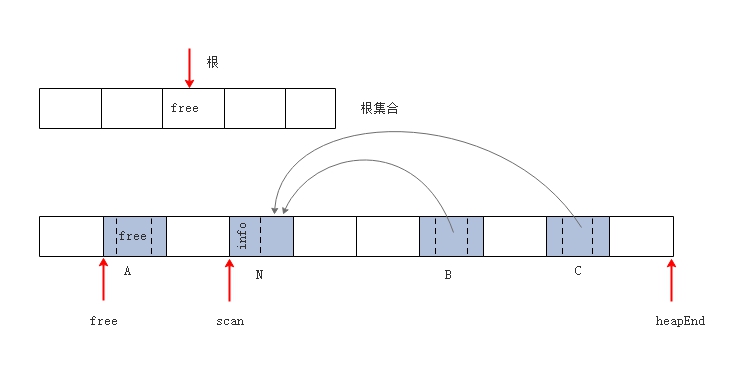 第一次遍历,扫描到对象 N,根据前向指针的引线,更新根对象及对象 A
的指针域(对象 N 的新地址 free1)。
第一次遍历,扫描到对象 N,根据前向指针的引线,更新根对象及对象 A
的指针域(对象 N 的新地址 free1)。 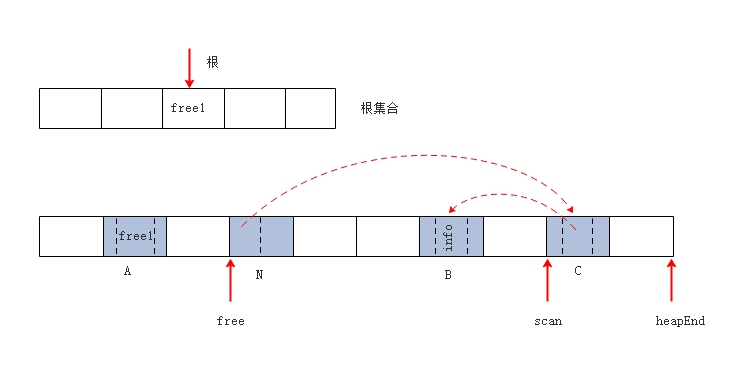 第一次遍历,扫描到对象
C,实现了后向指针的引线。
第一次遍历,扫描到对象
C,实现了后向指针的引线。 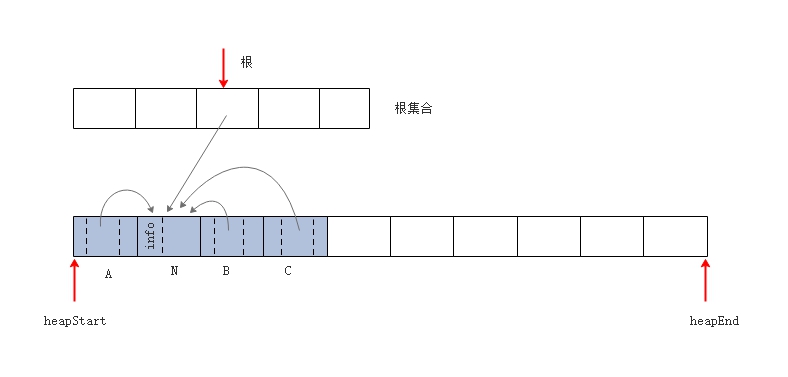 第二闪遍历,根据后向指针的引线,更新后向指针,且移动存活对象。
第二闪遍历,根据后向指针的引线,更新后向指针,且移动存活对象。
引线整理算法伪代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44compact():
updateForwardReferences() /* 更新前向指针 */
updateBackwardReferences() /* 更新后向指针 */
/* 对引用进行引线 */
thread(ref):
if *ref != null
*ref = **ref
**ref = ref
/* 根据引线,更新转发地址 */
update(ref, addr):
tmp = *ref
while isReference(tmp)
*tmp = addr
tmp = *tmp
*ref = tmp
/* 更新前向指针 */
updateForwardReferences():
for each fld in Roots
thread(*fld)
free = HeapStart
scan = HeapStart
while scan <= HeapEnd
if isMarked(scan)
update(scan, free) /* 将所有指向 scan 的前向指针都修改为 free */
for each fld in Pointers(scan)
thread(fld)
free = free + size(scan)
scan = scan + size(scan)
/* 更新后向指针且移动对象 */
updateBackwardReferences():
free = HeapStart
scan = HeapStart
while scan <= HeapEnd
if isMarked(scan)
update(scan, free) /* 将所有指向 scan 的后向指针都修改为 free */
move(scan, free)
free = free + size(scan)
scan = scan + size(scan)
2.4 单次遍历算法
在上面三种整理算法中,都需要多次遍历堆,有没有只需要遍历一次堆即可完成内存整理?借助额外的数据结构存储对象的“转发地址”,单次遍历算法通过一次堆的遍历便可实现内存的整理,这是典型的“空间换时间”。 在单次遍历算法中,使用了两种数据结构:1)标记位向量(mark-bit vector),它的每一位反映了每个存活对象的起始和结束地址;2)偏移向量(offset vector),将堆划分成大小相等的小内存块(分别是 256 字节和 512 字节),偏移向量记录了每一个内存块中第一个存活对象的的转发地址,其他存活对象的转发地址可以通过偏移向量和标记位向量实时计算得出。对于任意给定对象,可以先计算出其所在内存块的索引号,然后再根据该内存块在偏移向量和标记位向量中对应数据计算出该对象的转发地址。回收器不再需要两次遍历来移动对象和更新指针,转而可以通过对标记位向量的一次遍历来构造偏移向量,然后再通过一次堆遍历同时完成对象的移动和指针的更新。
以下图为例,假定每个内存块包含 8
个槽,每一个槽代表一个字,任意一个对象在标记位向量中使用起始和结束地址进行标记,如old对象,在标记位向量中使用第
16 位和第 19 位来标记。 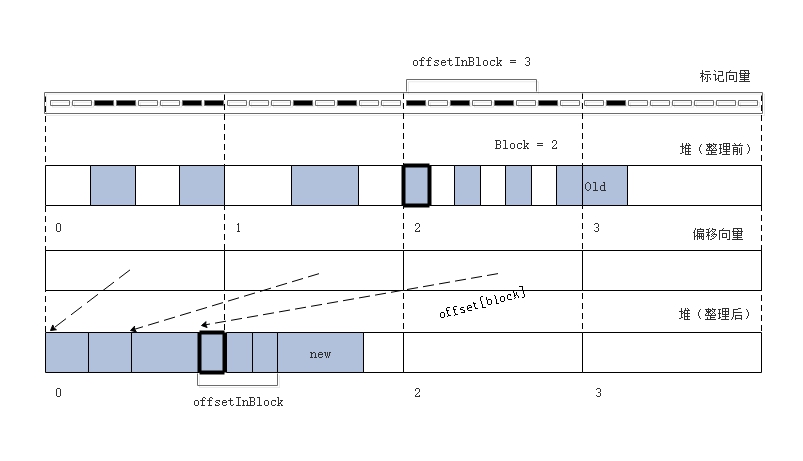 在上图中,堆被分成 4
个内存块,分别是 block 0~3,block 0 中的第 2、3、6、7位被设置,block 1
中的第 3、5 位被设置,这表示已经有 7
个内存字在标记位向量中得到了标记,因此 block 2
中的第一个存活对象将被移动到堆中的第 7 个槽中,对应 offset [ 2(block) ]
= 7, old 对象在 block 2 中的偏移 offsetInBlock(old) = 3, 那么 old
对象的转发地址就等于 offset[2] + offsetInBlock(old) = 10。
在上图中,堆被分成 4
个内存块,分别是 block 0~3,block 0 中的第 2、3、6、7位被设置,block 1
中的第 3、5 位被设置,这表示已经有 7
个内存字在标记位向量中得到了标记,因此 block 2
中的第一个存活对象将被移动到堆中的第 7 个槽中,对应 offset [ 2(block) ]
= 7, old 对象在 block 2 中的偏移 offsetInBlock(old) = 3, 那么 old
对象的转发地址就等于 offset[2] + offsetInBlock(old) = 10。
单次遍历算法的流程如下:
- 根据标记过程中得到的标记位向量,计算偏移向量;
- 从头到尾遍历堆,根据标记位向量和偏移向量,计算出对象的转发地址,进行对象的移动或指针的更新。
单次遍历算法伪代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35compact():
computeLocations(HeapStart, HeapEnd, HeapStart) /* 计算偏移向量 */
updateReferencesRelocate(HeapStart, HeapEnd) /* 更新转发地址和移动对象 */
/* 计算偏移向量 */
computeLocations(start, end, toRegion)
loc = toRegion
block = getBlockNum(start) /* 得到指针所在块的索引 */
for b = 0 to numBits(start, end) - 1 /* 遍历标记位向量 */
if b % BITS_IN_BLOCK == 0 /* 是否跨越了块边界 */
offset[block] = loc /* 存放块中第一个对象的地址 loc */
block = block + 1
if bitmap[b] = MARKED
loc = loc + BYTES_PER_BIT /* 根据存活对象的大小移动 */
/* 计算转发地址 */
newAddress(old):
block = getBlockNum(old)
return offset[lock] + offsetInBlock(old) /* 转发地址的公式 */
updateReferencesRelocate(start, end):
for each fld in Roots
ref = *fld
if ref != null
*fld = newAddress(ref)
scan = start
while scan < end
scan = nextMarkedObect(scan) /* 使用位图 */
for each fld in Pointers(scan) /* 更新引用 */
ref = *fld
if ref != null
*fld = newAddress(ref)
dest = newAddress(scan)
move(scan, dest)
3. 复制式回收算法
相对于标记 - 整理算法,复制式回收算法,可以有效提供内存分配的效率,同时回收过程只需要遍历堆一次,其缺点是堆的可用空间降低了一半。基本的复制式回收器将堆划分为两个大小相等的半区(semispace),分别是来源空间(fromspace)和目标空间(tospace),为了简化,我们假定堆是一块连续的内存空间。当堆空间足够时,在目标空间中分配新对象的方法是根据对象的大小简单地增加空闲空间,如果可用空间不足,则进行垃圾回收。回收器先两个半区角色进行切换,然后将存活对象从来源空间得到到目标空间。在回收完成之后,所有存活对象将紧密排布在目标空间的一端。在下一轮回收之前,回收器将简单地丢弃来源空间(为了安全起见,可以作清零处理)。
复制式回收算法的流程如下:
- 初始化工作列表(栈结构),将复制完成但未扫描的对象(灰色对象)放入工作列表,列表为空表示结束;
- 从根集合开始,将根对象复制到目标空间,在原有对象中设置转发地址,即目标空间的新地址,并将根对象放入工作列表中,原对象中是否有转发地址是判断复制是否完成的依据;
- 从工作列表中取出灰色对象,扫描其指针域,将指针指向的对象复制到目标空间中,设置转发地址,并加入工作列表;
- 重复第 3 步操作,直到工作列表为空。
Cheney 扫描(Cheney scanning)算法是一种十分优雅的算法,该算法复用目标空间中的灰色对象实现栈的结构,它仅需要一个指针 scan 为指向下一个待扫描对象,除此之外不再需要任何额外空间。结束的标志是指针 scan 和指针 free 重合。
下面是一个 Cheney 扫描对象 L
的实例,该对象是链表结构的头结点,它包含指向表头和表尾的指针。 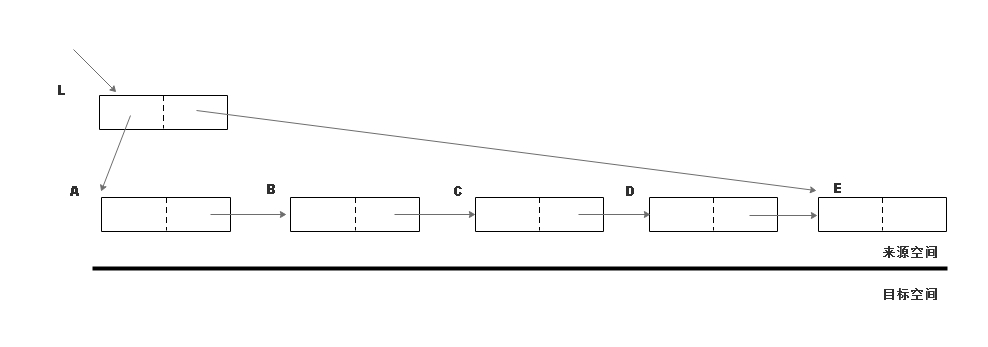 初始状态,所有对象都在来源空间。
初始状态,所有对象都在来源空间。 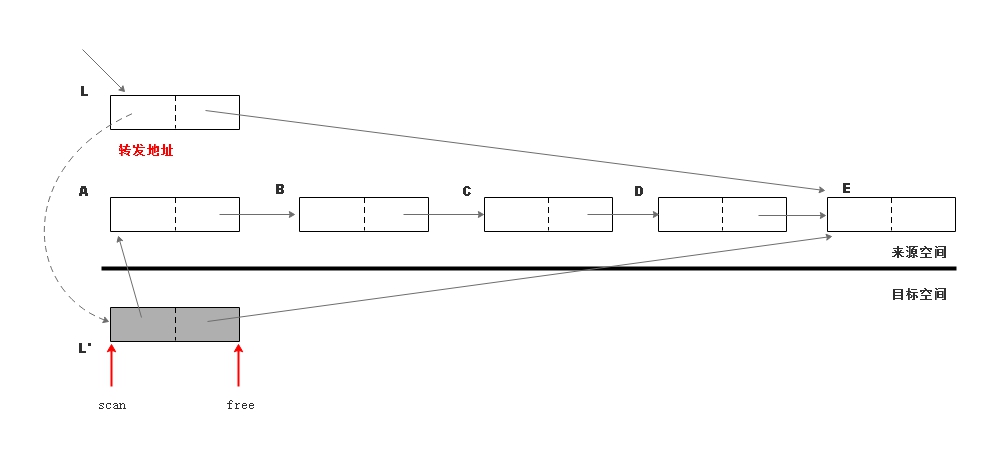 复制根对象,使用原对象的头部存放转发地址。
复制根对象,使用原对象的头部存放转发地址。
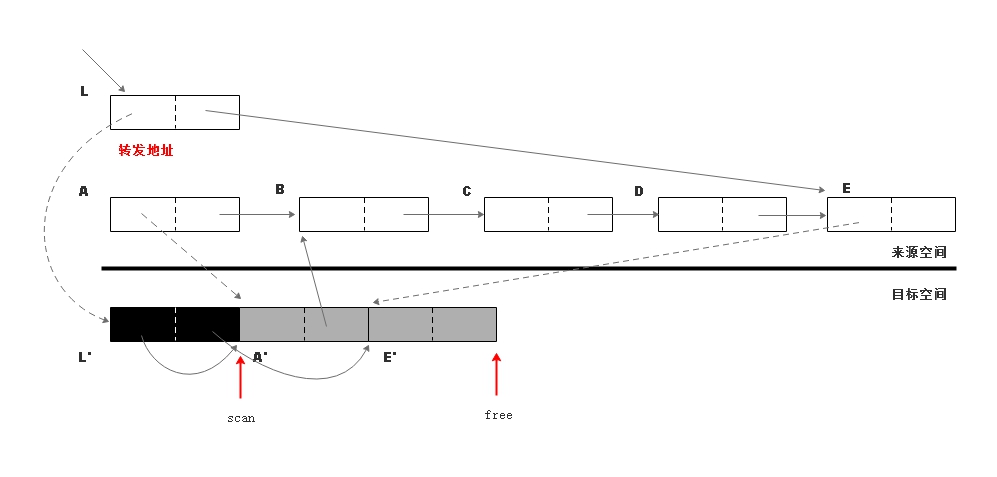 扫描根对象副本 L' 的指针域,复制 A、E
对象到目标空间,扫描结束,根对象副本 L' 出栈,继续对 A 对副本 A'
象进行扫描。
扫描根对象副本 L' 的指针域,复制 A、E
对象到目标空间,扫描结束,根对象副本 L' 出栈,继续对 A 对副本 A'
象进行扫描。 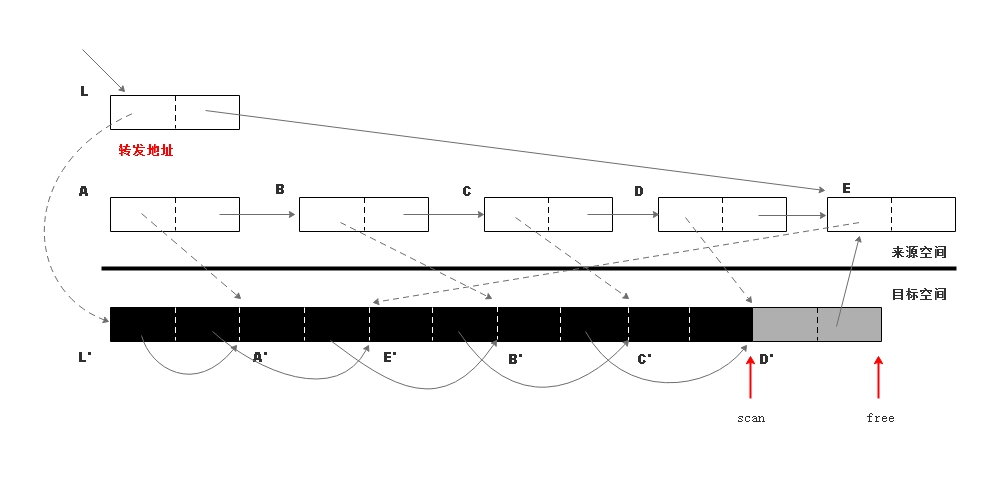 扫描对象 C 副本 C'
扫描对象 C 副本 C'
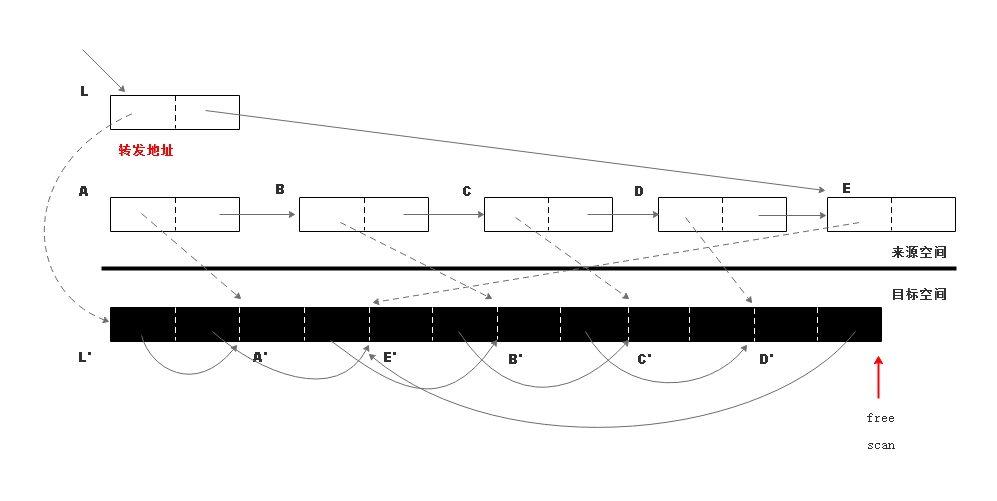 扫描对象 D 副本 D',此时 scan =
free,说明回收结束。
扫描对象 D 副本 D',此时 scan =
free,说明回收结束。
复制式回收算法伪代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79/* 创建半区 */
createSemispaces():
tospace = HeapStart
extent = ( HeapEnd - HeapStart ) / 2
top = fromspace = HeapStart + extent
free = tospace
/* 分配内存 */
allocate(size):
result = free
newfree = result + size
if newfree > top
return null /* 内存耗尽 */
free = newfree
return result
/* 内存整理 */
collect():
flip() /* 切换来源空间和目标空间 */
initialise(worklist) /* 将工作列表初始化为空 */
for each fld in Roots /* 复制根 */
process(fld)
while not isEmpty(worklist)
ref = remove(worklist)
scan(ref)
/* 翻转半区 */
flip():
tmp = fromsapce
fromspace = tospace
tospace - tmp
top = tospace + extent
free = tospace
scan(ref):
for each fld in Pointers(ref)
process(fld)
/* 使用目标空间中新副本的地址来更新域 */
process(fld):
fromRef = *fld
if fromRef != null
*fld = forward(fromRef) /* 使用目标空间中新副本的地址来更新 */
forward(fromRef):
toRef = forwardingAddress(fromRef)
if toRef = null /* 尚未得到复制(尚未标记) */
toRef = copy(fromRef)
return toRef
/* 复制对象,返回转发地址 */
copy(fromRef):
toRef = free
free = free + size(fromRef)
move(fromRef, toRef)
forwardingAddress(fromRef) = toRef /* 标记 */
add(worklist, toRef)
return toRef
/* 使用 Cheney 工作列表进行复制 */
initialise(worklist):
scan = free
isEmpty(worklist):
return scan = free
remove(worklist):
ref = scan
scan = scan + size(scan)
return ref
add(worklist, ref):
/* 空 */
4. 引用计数算法
上面讲到的三种垃圾回收算法都是间接式的,它们需要从已知的根集合出发对存活对象进行遍历,进而才能确定所有的存活对象。而在引用计数算法中,对象的存活性可以通过引用关系的创建或删除直接判定,无须像上面的三种追踪式回收器那样先通过堆遍历找出所有的存活对象,然后再反向确定出未遍历到的垃圾对象。
引用计数算法判断一个对象是否回收的依据是:当且仅当指向某个对象的引用数量大于零时,该对象才有可能是存活的。在引用计数算法中,每个对象都需要与一个引用计数相关联,这一计数通常保存在对象头部的某个槽中。下面是一个简单的引用计数算法,Write方法用于增加新目标对象的引用计数,同时减少旧目标对象的引用计数。对象执行读写操作时,需要维护其关联的引用计数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24New():
ref = allocate()
if ref = null
error "Out of memory"
rc(ref) = 0 /* 初始化计数 */
return ref
Write(src, i, ref):
addReference(ref)
deleteReference(src[i])
src[i] = ref
addReference(ref):
if ref != null
rc(ref) = rc(ref) + 1
deleteReference(ref):
if ref != null
rc(ref) = rc(ref) - 1
if rc(ref) = 0
for each fld in Pointers(ref)
deleteReference(*fld)
free(ref)
引用计数算法将内存管理开销分摊在程序运行过程中,无须停顿程序便可对内存进行整理,也不用为回收器预留一定空间。另外一方面也不需要运行时系统的支持,以库的形式就可以支持内存的回收,如 C++ 的智能指针就是使用引用计数来实现内存的自动管理。除了这些优点,引用计数算法同样存在一些缺陷:1)引用计数给赋值操作带来了额外的时间开销,因为需要维护引用计数;2)引入多线程竞争的问题,引用计数的增减操作以及加载和存储指针的操作必须是原子化的;3)读操作会引发计数器的更新操作,会“污染”高速缓存;4)引用计数无法回收环状引用数据结构;5)引用计数会占用额外的存储空间。
注:环状垃圾回收的问题,一般需要引入停顿程序的方式来解决。
5. 总结
本篇文章分析了四种基本的垃圾回收算法,它们分别有不同的使用场景:
- 标记 - 清扫: 算法简单,适合于分配固定大小对象的场景;
- 标记 - 整理: 需要遍历堆多次或引入额外的数据结构来记录转发地址,算法较复杂,优势是可以解决内存碎片的问题,内存利用率较高;
- 复制式回收算法 : 内存分配速度及效率较高,缺点是堆的可用空间降低了一半;
- 引用计数:内存管理的开销分摊到程序运行期间,不需要运行时系统的支持,但需要解决环状引用的问题。
参考: