神经网络:Hello World
看了《Python神经网络编程》之后,按照书上的代码,编写了一个用于识别手写数字的神经网络程序,算是神经网络的
Hello World 程序了。
概述
神经网络是一种模拟人脑的神经网络,以便实现类人工智能的机器学习技术。计算机比较擅长做数值的计算,数值类或有固定逻辑(模式)的问题比较容易转化为计算机的指令,从而快速的执行并给出答案。不过在另外一些场景下,对于人类而言很简单的问题,如图像分类或语音识别,计算机却很难给出答案。通常情况下,图像和音频文件包含大量的信息,通过普通的方法很难找出特定的模式来有效解决此类问题,而神经网络算法的出现,则为解决此类问题提供了可能。
基本概念
- 神经元(Neuron) 神经网络的基本单元,每个神经元接收一组输入值,进行加权求和,并可能添加一个偏置项。
- 层(Layer) 神经元的集合,通常分为输入层、隐藏层和输出层。输入层接收原始数据,隐藏层是中间层,可以有多个,用于提取特征和进行非线性变换,输出层产生最终的预测或分类结果。
- 权重(Weight) 每个神经元的输入都有一个权重,这些权重决定了输入信号对神经元输出的影响大小。
- 偏置(Bias) 加在加权求和的输入上的一个值,用于调整神经元激活的阈值。
- 激活函数(Activation Function) 一个数学函数,用于在神经元的加权求和之后引入非线性,使得网络能够学习和执行更复杂的任务。常见的激活函数包括 Sigmoid、Tanh、ReLU(Rectified Linear Unit)等。
- 前向传播(Forward Propagation) 数据在神经网络中的流动方向,从输入层通过隐藏层到输出层。
- 损失函数(Loss Function) 衡量模型预测值与实际值差异的函数,用于指导模型训练过程中的优化。
- 反向传播(Backpropagation) 一种训练神经网络的算法,通过计算损失函数关于网络参数的梯度,并利用这些梯度来更新网络的权重和偏置。
- 优化器(Optimizer) 用于在训练过程中更新网络权重的算法,如梯度下降、Adam、RMSprop 等。
- 训练(Training) 使用大量数据和损失函数来调整网络权重和偏置,使模型能够准确地预测或分类新数据。
- 过拟合(Overfitting) 模型在训练数据上表现很好,但在未见过的数据上表现差,即模型对训练数据过度学习。
- 正则化(Regularization) 一种技术,用于减少过拟合,如 L1、L2 正则化或 Dropout。
- 学习率(Learning Rate) 学习率是一个标量值,用于乘以损失函数关于模型参数的梯度。这个乘积决定了在每次迭代中更新模型参数的步长。
神经网络的起源
神经元
在理解神经网络之前,我们首先需要了解神经元,这是神经网络的基本元素。神经元是生物神经系统的工作单位,也是人工神经网络的灵感来源。
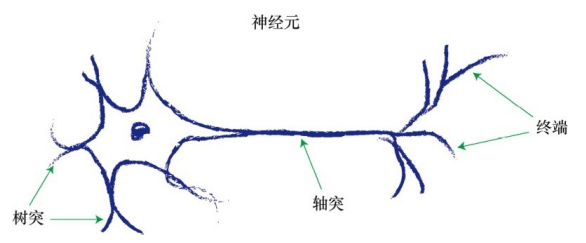
- 神经元的结构:每个神经元都由细胞体、树突、轴突和终端组成。细胞体包含核心部分,树突接收来自其他神经元的信号,而轴突将信号传递给其他神经元;
- 信号传递:神经元之间的通信是通过电信号完成的。当信号通过树突传递到细胞体时,如果达到一定阈值,神经元就会触发并将信号传递给下一个神经元。
一般来说,人类大脑大约有 1000
亿个神经元,这些神经元彼此之间通过协作,完成了传统计算机无法完成的工作。树突收集电信号,将其组合形成更强的电信号。如果电信号足够强,超过阈值,神经元就会发射信号,沿着轴突,到达终端,将信号传递给下一个神经元的树突。
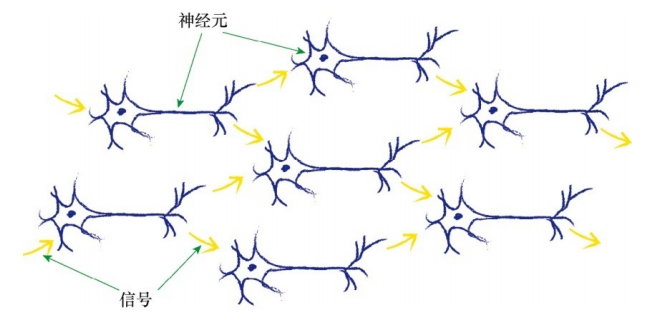
需要注意的一点是,每一个神经元接受来自其之前多个神经元的输入,并且如果神经元被激发了,它也同时提供信号给更多的神经元。
人工神经元
现在,让我们将生物神经元的概念转化为数学模型,即人工神经元。人工神经元是神经网络的基本元素,负责对输入进行处理和传递信号。输入可以类比为神经元的树突,而输出可以类比为神经元的轴突,计算则可以类比为细胞核。
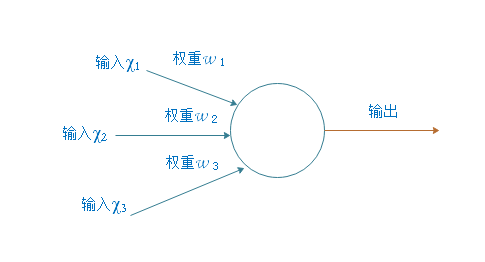
- 输入和权重:人工神经元接收多个输入,每个输入都有一个相关联的权重,这相当于人工神经网络的记忆。这些权重决定了每个输入对神经元的影响程度。
基础的神经元没有偏置 b 参数,相对来说,带偏置 b
参数的神经元更为常见。在本文中,为了计算的简便,我们使用基础版本的神经元,不带偏置
b 参数。 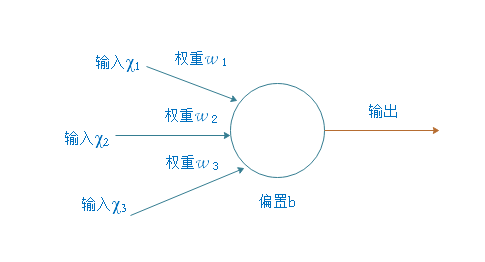
- 激活函数:在人工神经元中,激活函数决定了神经元是否激活(发送信号)。常见的激活函数包括
Sigmoid、ReLU 和 Tanh。在该文中我们使用 Sigmoid 函数。
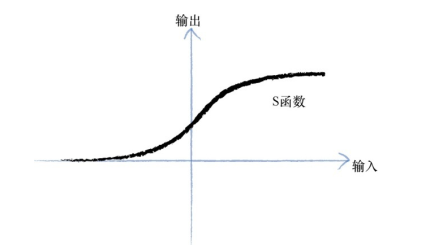
在这里,把 Sigmoid 函数称为 S
函数,该函数变化相对比较平滑,更自然也更接近现实。S
函数也称为逻辑函数,函数值在 (0, 1) 取值范围内。 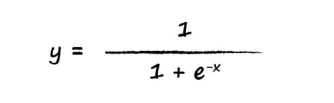
总的来说,可以把一个神经元看成一个由输入值和权重组成的函数,输入值和权重按照一定规则组合得到一个
X 值(组合规则可以是输入值和权重两两相乘再相加,或许也有其它规则),再将
X 值作为参数传入 S
函数,最终输出一个值,该值作为神经元的输出值,并作为下一个神经元的输入值,传递下去。
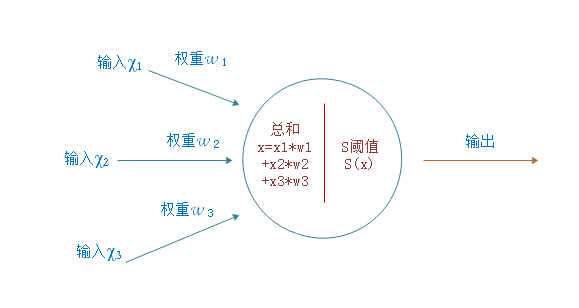
通过上述方法,我们得到了单个神经元的模型,但一个神经元的作用是有限的,与生物神经元一样,只有将它们组合起来形成一个神经元网络,才能发挥作用。
如同生物神经元一样,我们构建多层神经元,每一层中的神经元都与在其后层的神经元互相连接。如下图三层神经元网络中,每一层有三个人工神经元节点,每一个结点都与前一层或后续层的其他每一个结点相连接。
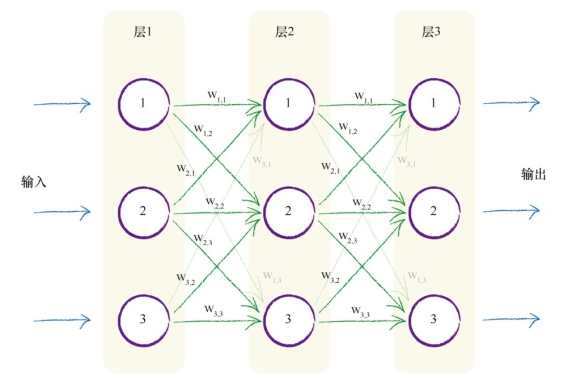
层与层之间的连接我们赋予了一个权重,表示信号的连接强度。需要注意的一点是,一个结点会连接到下一层的所有结点,有些连接可能是不必要的,但没有关系,可以通过赋予一个很小的权重值来达到这个目的。
总的来说,一个多层神经网络代表一个函数
f,其输出为函数值,输入和权重代表了这个函数的自变量。可以简略的表示为:
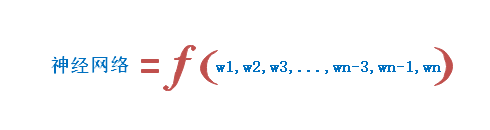
神经网络如何工作
前向传播信号
前向传播主要是将输入转化为输出的过程,输入的值作为第一层的结点,将输入值传递给第二层的结点,第二层结点的输出再作为第三层结点的输入,依次类推,从而得出最终的输出结果。单个结点的计算的方式在上文已经讨论过,如下所示:
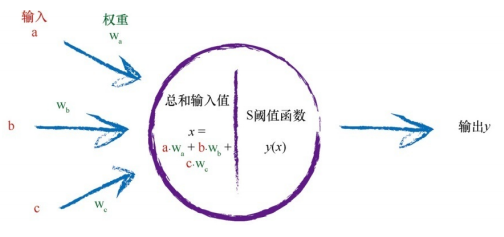
计算输出包含两个步骤:
- 计算总和:输入与权重两两相乘再相加;
- 计算阈值:将总和输入到 S 函数,计算输出。
以二层神经网络为例,我们来计算结点的输出。 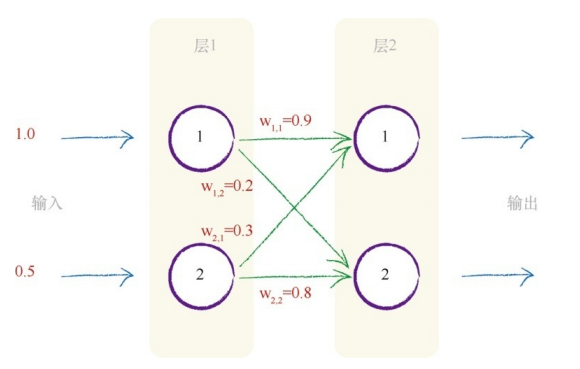
其中输入和权重都是随机值,合适的取值范围后面内容再讨论。神经网络初始的变量都是随机值,这些随机值会随着训练的进行而得到调整和优化,最终得到较优的值。所以,权重取随机重本身没有问题,而输入值一般是真实的数据,如一张图片数据,在这里,为了演示计算的过程,也取了随机值。
第一层节点是输入层,这一层不做其他事情,仅表示输入信号,也就是说,输入结点不对输入值应用激活函数。 第二层节点需要计算每一个结点的输出,其计算包含两个步骤:1)计算总和;2)对总和应用激活函数。下面我们来计算第二层两个结点的输出。 第一个结点: 1)计算总和 x = (上一层第一个节点的的输出 * 链接权重) + (上一层第二个结点的输出 * 连接权重) x = (1.0 * 0.9) + (0.5 * 0.3) = 1.05 2)应用激活函数 y = S(1.05) = 0.748
第二个结点: 1)计算总和 x = (上一层第一个节点的的输出 * 链接权重) + (上一层第二个结点的输出 * 连接权重) x = (1.0 * 0.2) + (0.5 * 0.8) = 0.6 2)应用激活函数 y = S(0.6) = 0.6457
下图显示了我们最终计算得到的输出。 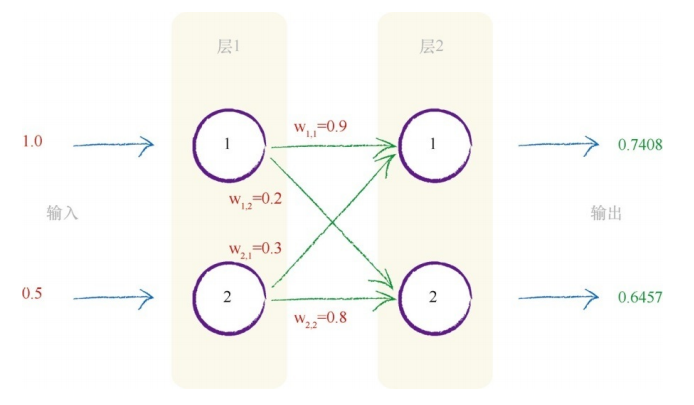
这是一个二层网络的计算过程,因为结点和层数较少,计算量不是很多,但对有较多结点和层数的神经网络而言,这样的计算方式显得繁琐且不高效,有没有更好的计算方式?答案是显而易见的,那就是使用矩阵来简化计算流程。
使用矩阵乘法计算输出输出值
可以将第二层结点的总和通过如下的矩阵一次性计算出来。 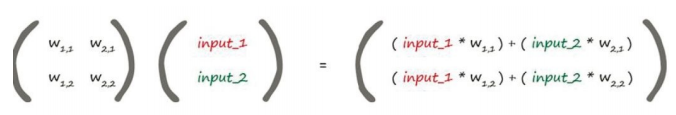
第一个矩阵包含两层结点之间的权重,第二个矩阵包含第一层输入层的信号,通过两个矩阵相乘,我们得到的答案是输入到第二层节点组合调节后的信号。由权重 w1,1 乘以 input_1 加上权重 w2,1 乘以 input_2,就是第二层第一个节点的输入值,这些值就是在应用 S 函数之前的 x 的值。
下图明确展示了它们之间的关系。 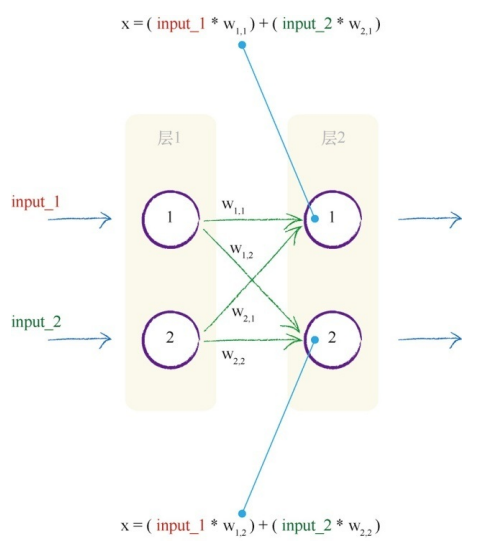
我们可以使用如下的公式来表示这个计算过程: 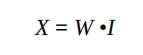
其中,W 是权重矩阵,I 是输入矩阵,X 是总和的矩阵,即输入到第二层的结果矩阵。矩阵通常使用斜体显示,表示它们是矩阵,而不是单个数字。
我们已经得到了结果矩阵,还需要将它应用到激活函数 S
中,从而这一层的输出矩阵,可以用以下的公式表示: 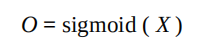
斜体的 O 代表矩阵,这个矩阵包含了最终的输出结果。
矩阵的计算可以应用到非输入层中,大大提高了计算的效率。
总结
- 神经网络向前传播信号所需的大量运算可以表示为矩阵乘法;
- 不管神经网络的规模如何,将输入输出表达为矩阵乘法,使得我们可以更简洁地进行书写。
反向传递误差
当我们通过前向传播将输入转化为输出之后,真实的结果与输出结果之间在存在一个误差,该误差称为输出误差。接下来需要通过输出误差来调整权重值,第一步反向传递误差,将误差分摊到前面各层的结点中。一般情况下,输出和误差是多个节点共同作用的结果时,如何分摊误差呢?
有两种思想,一种是平分误差,即每一个结点得到相同的误差值(1 / 链接数量
* 输出误差),
另一种思想是权重比例分割误差,它为较大链接权重的链接分配更多的误差,因为这些链接对造成误差的贡献较大,如下图所示:
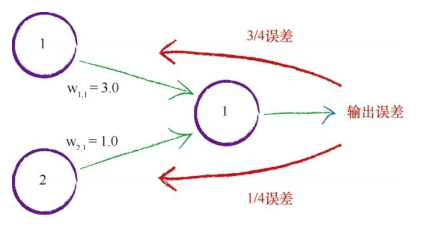
此处,有两个节点对输出节点的信号做出了贡献,它们的链接权重分别是 3.0
和 1.0,按照权重比例分割误差,那么节点 1 得到 3.0 / (1.0 + 3.0) 即 3 / 4
的误差,而节点 2 得到 1 / 4 的误差,计算公式如下图所示: 节点 1 的误差:

节点 2 的误差: 
我们可以将同样的思想扩展到多个结点,比如 100 个结点,那么我们要在这 100 条链接之间,按照每条链接对误差所做贡献的比例(由链接权重的大小表示),分割误差。
我们选用权重比例分割误差,这种思想比较合理。在神经网络中,在两件事情上使用了权重。第一件事情,使用权重,将信号从输入层向前传播到输出层。第二件事情,使用权重,将误差从输出向后传播到网络中,我们称这这种方法为反向传播。
多个输出节点反向传播误差
在神经网络中,一般都有多个输出结点,每一个结点都会产生误差,如下图展示了具有
2 个输入结点和 2 个输出结点的简单网络。 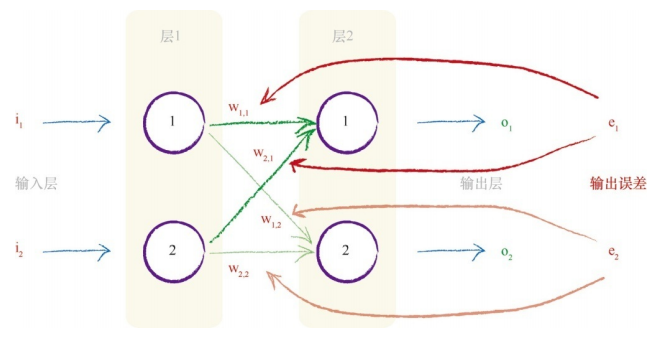
其中,o1 表示第一个输出结点的输出值,e1 表示输出结点 1 输出误差,它是期望的输出值 t1 与实际输出值 o1 之间的差,也就是 e1 = ( t1 - o1 )。而 o2 及 e2 表示第二个输出结点的输出值及输出误差。
从图中,按照链接的比例,也就是权重 w1,1 和 w2,1,对 e1 进行了分割。类似地,按照权重 w1,2 和 w2,2 对 e2 进行了分割。
从层 1 的结点 1 来看,它通过 w1,1 和 w1,2
链接,分别对两个输出结点贡献了误差,所以,它需要按照比例公摊
e1 和 e2 的值,即: 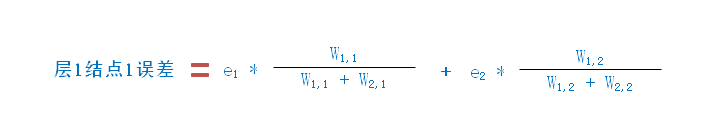
结点2的误差为: 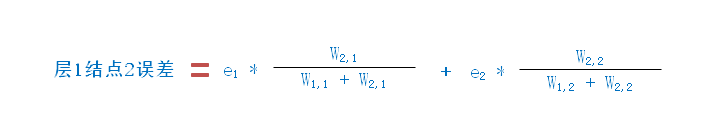
以此类推,在多层网络中,前一层的输出误差都可以通过后一层的输出误差及这两层的链接权重计算得出。
使用矩阵乘法进行反向传播误差
我们使用 erroroutput 表示输出误差,如下图所示: 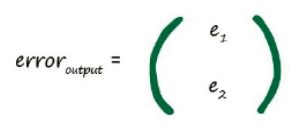
errorhidden
表示隐藏层的误差值,隐藏层是指非输出层和输入层的中间层,在这里泛指中间层,按照链接权重分割输出误差,其计算公式如下:
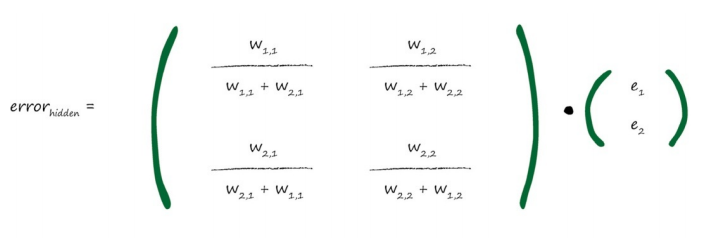 在这个矩阵中,这些分数比较难处理,不方便计算。考虑到,我们并不需要准确的计算值,只需要按比例分割误差即可,可以使用
e1 * w1,1 来代替 e1 * w1,1
/( w1,1 + w2,1),从而简化计算。
在这个矩阵中,这些分数比较难处理,不方便计算。考虑到,我们并不需要准确的计算值,只需要按比例分割误差即可,可以使用
e1 * w1,1 来代替 e1 * w1,1
/( w1,1 + w2,1),从而简化计算。 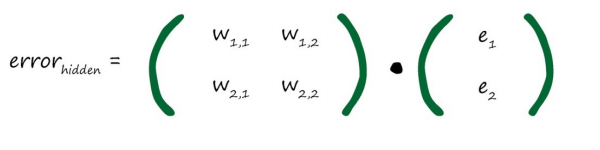
这个权重矩阵与隐藏层到输出层之间的链接权重矩阵相似,但是这个矩阵沿对角线进行了翻转,这样的矩阵我们称为转置矩阵,记为wT。最终的计算公式如下图所示:

总结
- 反向传播误差可以表示为矩阵乘法;
- 无论网络规模大小,这使我们能够简洁地表达反向传播误差;
- 这意味着前向传播信号和反向传播误差都可以使用矩阵计算而变得高效。
更新权重
到目前为止,我们已经将误差反向传播到网络的每一层。为什么这样做呢?原因就是,我们使用误差来指导如何调整链接权重,从而改进神经网络输出的总体方案。之前说过,神经网络是一个关于链接权重的函数,以一个简单的
3 层、每层 3 个结点的神经网络为例,其输出层可以用以下公式表达: 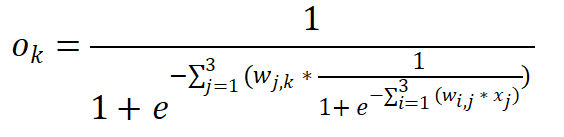
在这个 3 层网络中,其中输入层节点的输出是输入值和链接权重的函数。在节点 i 处的输入是 xi, 连接输入层节点 i 到中间层(隐藏层)节点 j 的链接权重为 wi,j,类似地,隐藏层节点 j 的输出是 xj,连接隐藏节点 j 和 输出层结点 k 的链接权重是 wj,k,求和表达式则是对所有后续表达式求和。
针对这样一个公式,我们要做的是通过某种方式找到好的权重组合。简单的做法是使用暴力方法,遍历每一种可能的权重组合。假设每一个权重在 -1 和 +1 之间有 1000 种可能的值,如 0.402、-0.324 和 0.457。对么对于 3 层、每层 3 个节点的神经网络,我们可以得到 18 个权重,因此有 1018 种可能性需要测试。结果层次数、结点数更多,则测试的可能性更多。
你会发现这种暴力方法不切实际,那有没有一种更好的办法呢?
梯度下降
所有权重组合生成的神经网络输出函数过于复杂,难以求解。太多的权重组合,难以逐个测试,不容易找到一种最好的组合。现在换一种思路,我们不要求取得最优解,取得近似解也可以。假设将一个复杂的多元函数类比为一个非常复杂、有波峰波谷以及连绵的群山峻岭,求函数最小值类比为从山坡走到坡底。在黑暗中,伸手不见五指,你知道你是在一个山坡上,你需要到坡底。对于整个地形,你没有精确的地图,只有一把手电筒。你能做什么呢?你可能会使用手电筒,做近距离的观察。手电筒看得不远,无论如何,你肯定看不到整个地形,你可以看到某一块土地看起来是下坡,于是你就小步地往这个方向走。通过这种方式,你不需要完整的地图,也不需要事先制定路线,你一步一个脚印,缓慢地前进,慢慢地下山。
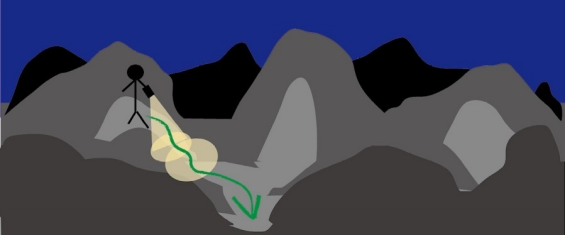
在数学上,这种方法称为梯度下降(gradient descent)。在你迈出一步之后,再次观察周围的地形,看看你下一步往哪个方向走,才能更接近目标,然后,你就往那个方向走出一步。你一直保持这种方式,直到最后到达了山底。梯度是指地面的坡度,你走的方向即坡度向下的方向。
现在,想象一下,这个复杂的地形是一个数学函数,梯度下降算法给我们带来一种能力,即我们不必完全理解复杂的函数,从数学上对函数进行求解,就可以找到最小值。如果函数非常困难,我们不能用代数轻松找到最小值,我们就可以使用这个方法来代替代数方法。当然,由于我们采用步进的方式接近答案,一点一点地改进所在的位置,因此这可能无法给出精确解。但是,这比得不到答案要好。总之,我们可以使用更小的步子朝着实际的最小值方向迈进,优化答案,直到我们对于所得到的精度感到满意为止。
梯度下降与神经网络之间有什么联系呢?我们将复杂困难的函数当作网络误差,那么下山找到最小值就意味着最少化误差。这样我们就可以改进网络输出,这就是我们想要的结果。
以函数 y = (x-1)2 + 1 为例,假设 y 表示误差,我们希望找到
x,可以最小化 y。 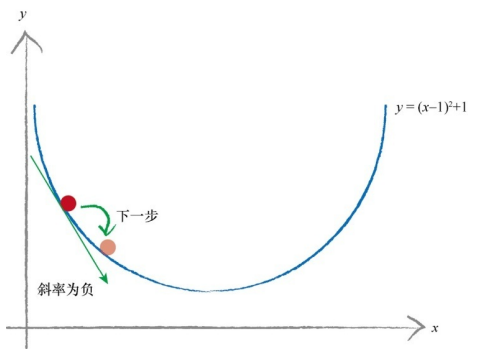
采用梯度下降算法,随机找一个起点。斜率表示坡度的方向,斜率为负表示下坡,我们稍微需要增加
x 的值。 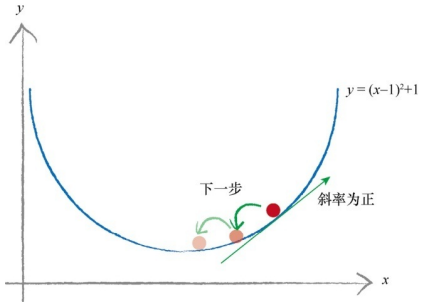
斜率为正表示上坡,我们反方向减小 x 的值。 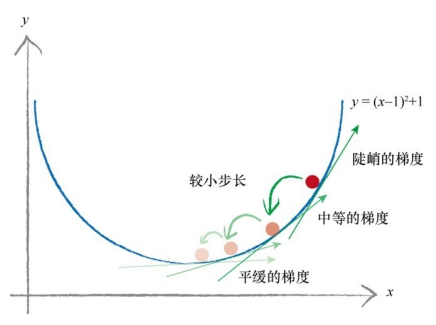
作为一个优化,我们需要根据坡度调整步子大小,这样可以避免超调,避免在最小值的地方来回反弹。步长调节可以与梯度的大小成比例,在接近最小值时,可以采用小步长。
当函数有很多参数时,梯度下降算法才真正地显现出它的优势,如神经网络的误差函数取决于许多的权重参数,这些参数通常有数百个。以二元函数为例,在这个三维空间里,我们使用高度来表示函数的值。
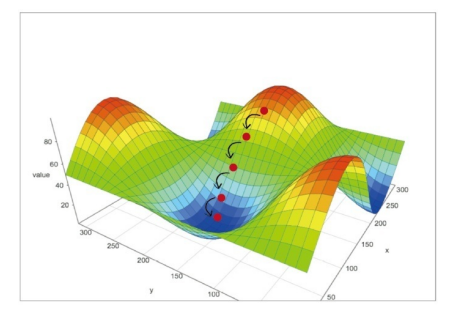
观察这个三维曲面,它有多个山谷,梯度下降会卡在错误的山谷吗?答案是肯定的,这种情况可能会发生,也就是所到达的山谷可能不是最低的山谷。
为了避免终止于错误的山谷或错误的函数最小值,我们从山上的不同点开始,多次训练神经网络,确保并不总是终止于错误的山谷。不同的起始点意味着选择不同的起始参数,在神经网络中,这意味着选择不同的起始链接权重。
下面详细说明了使用梯度下降方法的三种不同尝试,其中有一次,这种方法终止于错误的山谷中。
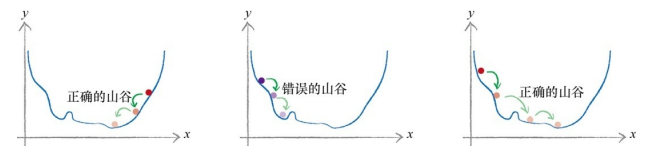
误差函数(损失函数)
神经网络的输出是一个极其复杂困难的函数,这个函数具有许多影响到其输出的链接权重参数。我们可以使用梯度下降方法,计算出正确的权重吗?只要我们选择了合适的误差函数,即损失函数,这是完全可以的。
神经网络本身的输出函数不是一个误差函数,不过误差是目标训练值与实际输出值之间的差值,因此可以很容易地将输出函数转化为误差函数。
下面有三种不同的误差函数选择: 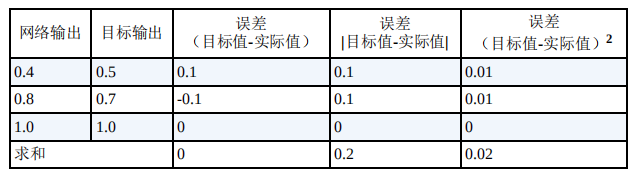
第一个选项是(目标值 - 实际值),这种方式比较简单,但有一个问题,正负误差相互抵消,得到的误差总和为 0。总和为 0 意味着没有误差,这明显不符合实际情况。 第二个选项是 | 目标值 - 实际值 |,这意味着可以无视符号,误差不会相互抵消,这可能行得通。不过这个函数在最小值附近是不连续的,这使得梯度下降方法无法很好地发挥作用。 第三个选项是差的平方,即 (目标值 - 实际值)2,这个误差函数有如下的优点,选择它是比较合理的。
- 使用误差的平方,可以很容易计算出梯度下降的斜率;
- 误差函数平滑连续,这使得梯度下降方法很好地发挥作用;
- 越接近最小值,梯度越小,这意味着,使用这个函数调节步长,超调的风险就会变得比较小。
是否还有第四个选择?答案是有,你可以构造不同的损失函数(也称为代价函数),特定的损失函数在特定的场景下可能发挥得更好,这就需要去验证。
我们可以用下图来表示链接权重与误差函数之间的关系(只演示了一个权重):
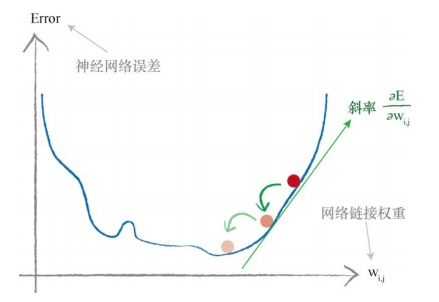
我们的目的是通过最小化神经网络的误差函数,来优化网络链接权重。沿着取得最小值的路上,一步一步到调整权重值的大小,在最终训练结束之后,得到较优化的权重值。知道了斜率,就可以对权重进行调整,调整用如下公式表示:
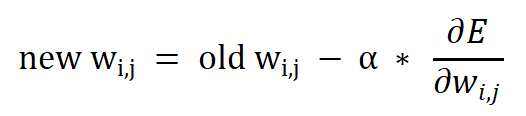
更新后的权重 wi,j 是通过误差斜率取反来调整旧的权重而得到的。如果斜率为正,则减少权重,如果斜率为负,则增加权重。符号 a 是一个因子,这个因子可以调节变化的强度,确保不会超调,通常称这个因子为学习率。
公式推导
在权重调整的公式中,斜率的计算非常关键,以下图为例,我们将推导斜率的计算公式。在这里先关注隐藏层和最终输出层之间的链接权重,输入层与隐藏层之间的权重调整与之相同,可以方便推广过去。
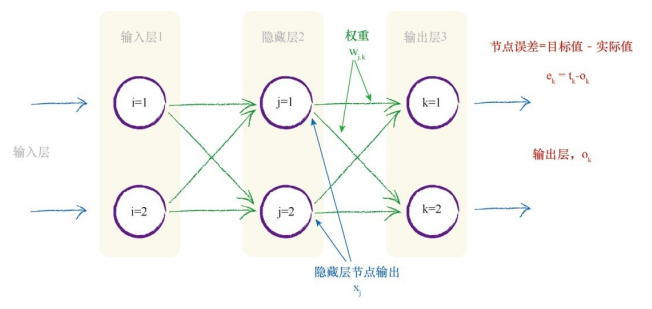
斜率表示为: 
这个表达式表示了当权重 wj,k 改变时,误差 E 是如何改变的。这是误差函数的斜率,也就是梯度下降方法中到达最小值的方向。
首先,展开误差函数,这是对目标值和实际值之差的平方进行求和,这是针对所有
n 个输出结点的和。 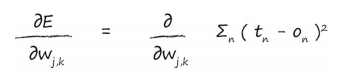
需要注意的是,在节点 n 的输出 on
只取决于连接到这个节点的链接,因此可以直接简化这个表达式。 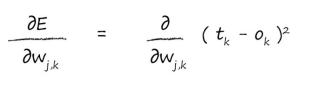
通过一系列的求解过程,最终得到斜率的求解表达式: 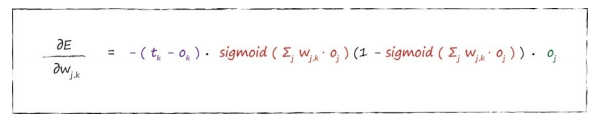
这个斜率表达式就是训练神经网络的关键。
这个表达式包含三个部分:
- 第一部分的(目标值 - 实际值)误差,现在变成了隐藏层节点中重组的向后传播误差,我们称为 ek。
- sigmoid 表达式的值就是 ok,即输出结点 k 的值。
- 最后一部分是第一层节点的输出 oj,即输入信号。
这个表达式不仅适用于隐藏层与输出层之间权重,而且适用于输入层和隐藏层之间的权重,也可以推广到更多层的神经网络中。
得到了斜率,我们可以计算调整后的值,表达式为: 
通过变换可以得到如下的表达式: 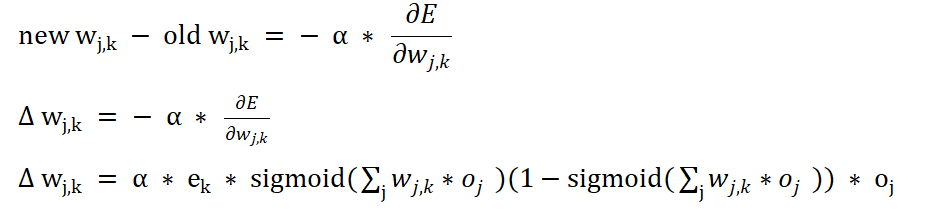
两次权重之间的差值称为误差梯度,借助矩阵可以高效地计算出一个任意两层之间的误差梯度,下图演示了计算的细节:
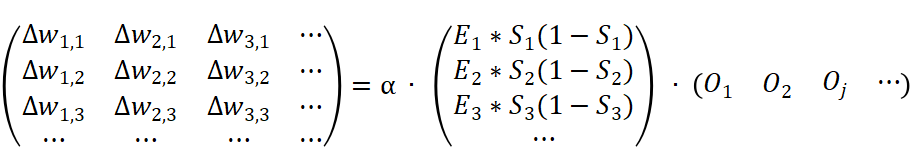
在上述矩阵中, Ek 表示反馈的误差值,Sk
表示输出结点 k 的值。 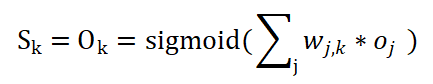
最后,我们用矩阵来表示出完整的误差梯度,这个公式可以通过计算机高效地实现。
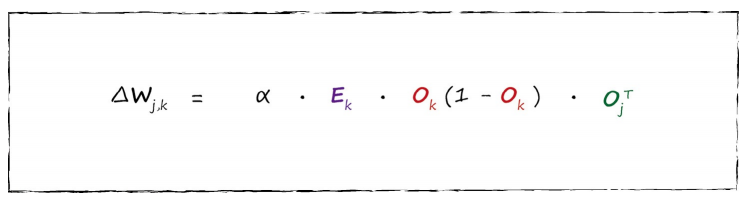
其中,Ek 表示层 j 的误差矩阵,Ok 表示层 k 的输出矩阵,OjT 表示层 j 的输入信号矩阵的转置矩阵。
权重更新范例
下面通过一个实例来演示权重更新的过程,当前的权重如下图所示: 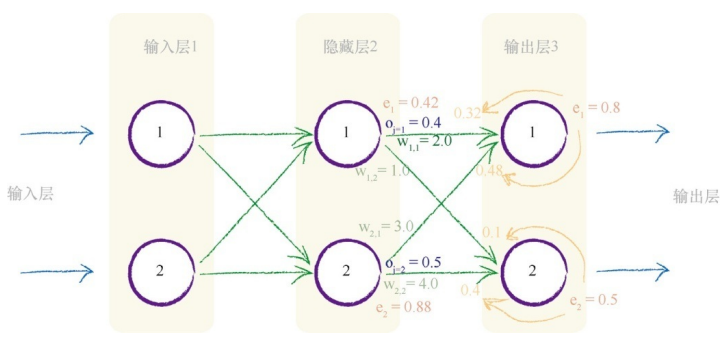
我们要更新隐藏层和输出层之间的权重 w1,1。当前这个值为
2.0,根据斜率公式: 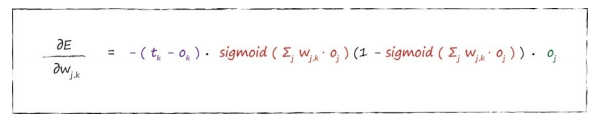
我们一项一项地进行运算:
- 第一项 (tk - ok)得到误差为 e1 = 0.8。
- S 函数内的求和为 (2.0 * 0.4) + (3.0 * 0.5)= 2.3。
- sigmoid(1/1+e-2.3) 为 0.909。中间的表达式为 0.909 * (1-0.909) = 0.083。
- w1,1 权重中,j=1,则 oj=1 = 0.4。
将三项相乘,-0.8 * 0.083 * 0.4 = - 0.0265。如果学习率为 0.1,那么得出的改变量为 - (0.1 * -0.02650) = + 0.002650。因此,新的 w1,1 就是原来的 2.0 加上 0.002650 等于 2.00265。
虽然这是一个相当小的变化量,但权重经过成百上千次的迭代,最终会确定下来,达到一种布局,这样训练有素的神经网络就会生成与训练样本中相同的输出。
总结
- 梯度下降算法是求解函数最小值的一种很好的办法,当函数非常复杂困难,并且不能轻易使用数学代数求解函数时,这种方法可以发挥很好的作用。
- 神经网络的误差是内部链接权重的函数,改进神经网络,意味着通过改变权重减小这种误差。
- 直接选择合适的权重太难了。另一种方法是,通过误差函数的梯度下降,采取小步长,迭代地改进权重。所迈出的每一步的方向都是在当前位置向下斜率最大的方向,这就是所谓的梯度下降。
初始数据的选择
开发设计一个良好的神经网络,需要准备好训练数据、初始随机权重及设计良好的输出方案, 这些方面的选择策略会影响到网络的成功与否。
输入
下图是 S
激活函数的图像,你可以发现,如果输入变大,激活函数就会变得非常平坦。
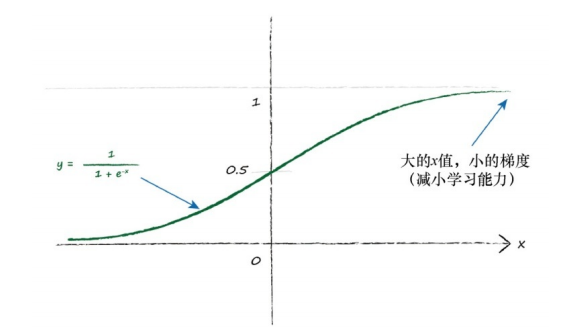
由于我们使用梯度学习新的权重,因此一个平坦的激活函数会出问题。
一个好的建议是将输入值控制在 0.0 到 1.0 之间的范围内,考虑到 0 值会生成学习能力的丧失(任何数乘以 0 都等于 0),因此输入不能为 0 , 建议在 0 的基础上加一个偏移,如 0.01。
输出
神经网络的输出是最后一层结点弹出的信号,我们使用的是 S 激活函数,其值范围为 (0.0, 1.0)。所以,常见的使用范围为 0.0 ~ 1.0 ,但是由于 0.0 和 1.0 这两个数也不可能达到,因此使用 0.01 ~ 0.99 范围。
初始权重
与输入和输出一样,同样的道理也适用于初始权重的设置。由于大的初始权重会造成大的信号传递给激活函数,导致网络饱和,从而降低网络学习到更好的权重的能力,因此应该避免大的初始权重值。
我们可以从 -1.0 ~ +1.0
之间随机均匀地选择初始权重,一个更好的经验法则是,我们可以在一个节点传入链接数量平方根倒数的大致范围内随机采样,初始化权重。假设每一个节点具有
3 条传入链接,那么初始权重的范围应该在从 -1/\(\sqrt{3}\) 到 +1/\(\sqrt{3}\),即
-0.577~+0.577之间。这一经验法则实际上讲的是,从均值
0、标准方差等于节点传入链接数量平方根倒数的正态分布中进行采样,如下图所示:
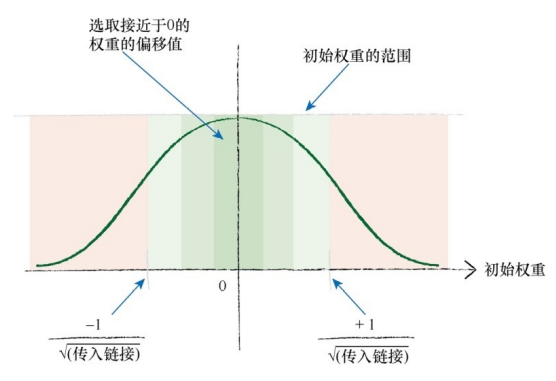
另外,需要注意的是, 禁止将初始权重设定为相同的桓定值,特别是禁止将初始值设定为 0.
开发环境搭建
本文使用 VS Code + Anaconda 环境开发。需要安装 VS Code 和 Anaconda 包,并将 VS Code 配置使用 Anaconda 环境,从而可以使用科学计算相关的包,如矩阵和图像处理等等。
VS Code 和 Anaconda 包的安装可参考官网,这里只演示下 VS Code 如何配置 Anaconda 环境:
- 打开 VS Code,并打开你要开发的工作区或文件夹;
- 使用快捷健 Ctrl+Shift+P 打开命令面板,输入并选择 Python: Select
Interpreter,在弹出的列表中,选择你的 Anaconda
环境。如果没有看到环境,点击 Enter interpreter path 并浏览到 Anaconda
环境中的 Python 可执行文件路径,通常是,Windows 安装目录为:
C:<username>.exe,macOS/Linux
安装目录为:/Users/
/anaconda3/envs/myenv/bin/python。 
- 大功告成。
程序介绍
程序目标
本文程序的目标主要是识别手写数字图片,图片内容如下图所示: 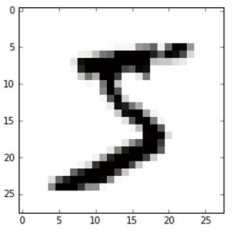
程序需要将该图片中的手写数字识别为 5。
输入
程序采用的数据集是 MNIST 数据库,网站为:http://yann.lecun.com/exdb/mnist/,不过由于 MNIST 数据库的格式不容易使用,因此其他人已经创建了相对简单的数据文件格式,参见 http://pjreddie.com/projects/mnist-in-csv/, 这对我们编写程序帮助很大。
这些文件称为 CSV 文件,这意味着纯文本中的每一个值都是由逗号分隔的。你可以轻松地在任何文本编辑器中查看这些数值。这个网站提供了两个 CSV 文件:
- 训练集 http://www.pjreddie.com/media/files/mnist_train.csv
- 测试集 http://www.pjreddie.com/media/files/mnist_test.csv
顾名思义,训练集是用来训练神经网络的 60 000 个标记样本集,标记是指输入与期望的输出匹配,也就是答案应该是多少。测试集包含了 10 000 个样本的数据,主要用来测试算法工作的好环程度。由于这也包含了正确的标记,因此可以观察神经网络是否得到正确的答案。
下面我们来看下文件的内容: 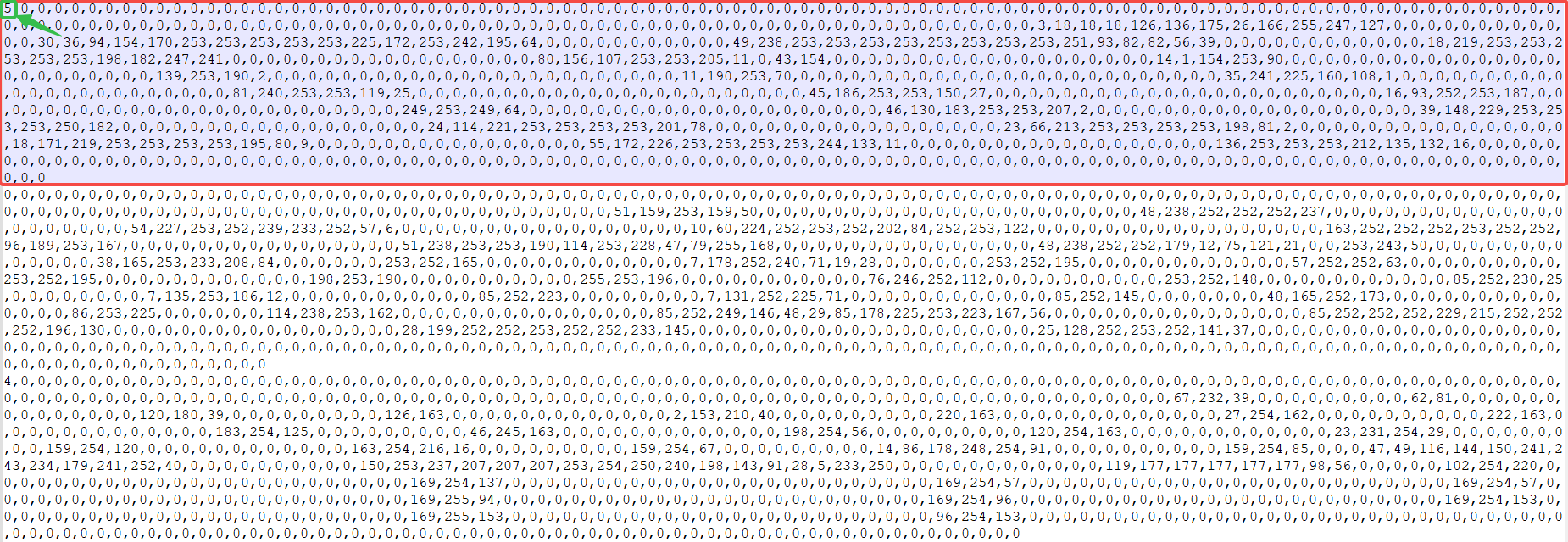
文件内容说明:
- 在 CSV 文件中,一行代表一副灰度图片数据;
- 每行的第一个值是标签,即图片代表的数字;
- 每行剩余的值,由逗号分隔,是手写体数字的像素值。像素数组的尺寸是 28 乘以 28,因此在标签后有 784 个值。
因此,第一行表示 5 的图像数据,第二行代表 0 的图像数据。
输出
神经网络的目的是识别 0~9
的手写体数字,很自然地,我们就可以想到输出层应该包含 10
个结点,每一个结点代表一个数字。如果答案是 "9",
输出层的最后结点会激发,而其余的输出结点则保持抑制状态。如下图所示:
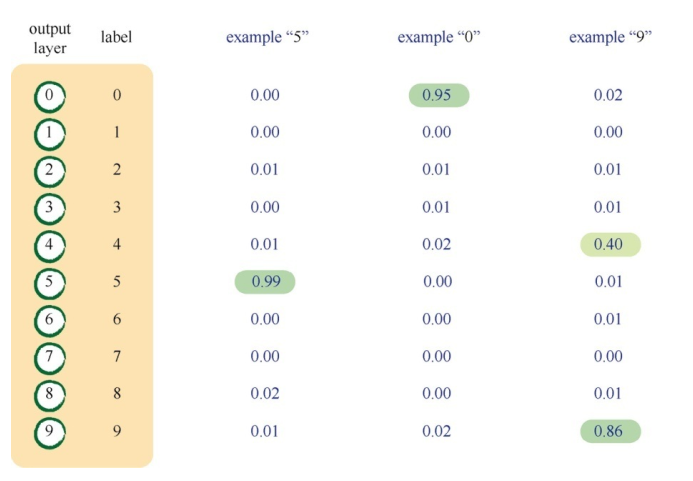
第一个示例是神经网络认为它看到的是数字 “5”,可以看到,从输出层出现的最大信号来自于标签为 5 的结点。由于标签从 0 开始,因此它是第六个结点。其余的输出结点产生的信号非常小,接近于零。但需要记住一点,不会存在零输出,即输出值不会为 0。 在第二个示例中,最大输出来源于 “0” 标签,它代表了该图像为 0 。在第三个示例中,有两个输出值相对比较大,说明在这里存在分歧,有可能是 4 或 9,在这里,通常选择最大输出的值。
确定了输出层的结点数,接下来,需要创建输出结点的目标数组,以标签 “5” 为例,除了对应于标签 “5” 的结点,其他结点的值应该都很小,这个数组看起来可能是这样 [0, 0, 0, 0, 0, 1, 0, 0, 0, 0],不过由于网络网络不能生成 0 和 1(激活函数输出值只能无限趋近于 0 或 1),因此需要重新调整这些数字,使用 0.01 和 0.99 来代替 0 和 1。这样标签为 “5” 的目标输出数组为 [0.01, 0.01, 0.01, 0.01, 0.01, 0.99, 0.01, 0.01, 0.01, 0.01]。
代码分析
这一节我们使用 Pyton 来实现经典的神经网络算法。
代码整体结构
代码主要分为三个部分:
- 初始化函数,设定输入层结点、隐藏结点和输出结点的数量;
- 训练,学习给定训练集样本后,优化权重;
- 查询,给定输入,从输出结点给出答案。
其框架代码如下所示:
1 | import numpy |
代码
完整代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213import numpy
import scipy.special
# neural network class definitioin
# 神经网络对象定义
class neuralNetork:
# initialise the neural network
# 初始化神经网络
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate) -> None:
# set number os nodes in each input, hidden, output layer
# 设置输入层结点、隐藏层结点及输出结点数量
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# learing rate
# 设置学习率
self.lr = learningrate
# link weight matrices, wih and who
# 初始化输入层与隐藏层结点的权重
self.wih = numpy.random.normal(
0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
# 初始化隐藏层与输出层结点的权重
self.who = numpy.random.normal(
0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
# activation function is the sigmoid function
# 设置激活函数为 sigmoid 函数
self.activation_function = lambda x: scipy.special.expit(x)
pass
# train the neural network
# 训练神经网络
def train(self, input_list, targets_list):
# convert inputs list to 2d array
# input_list 输入为 784个元素的数组,将它转换为 784 * 1 矩阵
inputs = numpy.array(input_list, ndmin=2).T
# targets_list 为 10 个元素的数组,将它转换为 10 * 1 矩阵
targets = numpy.array(targets_list, ndmin=2).T
# calculate signals into hidden layer
# 计算隐藏层的输入信号
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
# 计算隐藏层的输出信号
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
# 计算输出层的输入信号
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final opuput layer
# 使用激活函数,计算出输出层的输出信号
final_outputs = self.activation_function(final_inputs)
# output layer error is the (target - actual)
# 计算输出层的误差矩阵
output_errors = targets - final_outputs
# hidden layer error is the output_errors, split by weights, recombined at hidden nedes
# 反向传递计算隐藏层的误差矩阵
hidden_errors = numpy.dot(self.who.T, output_errors)
# update the weights for the links between the hidden and output layers
# 根据误差矩阵,更新隐藏层到输出层的权重
self.who += self.lr * numpy.dot((output_errors * final_outputs * (
1.0 - final_outputs)), numpy.transpose(hidden_outputs))
# update the weights for the links between the input and hidden layer
# 根据误差矩阵,更新输入层到隐藏层的权重
self.wih += self.lr * \
numpy.dot((hidden_errors * hidden_outputs *
(1.0 - hidden_outputs)), numpy.transpose(inputs))
pass
# query the neural network
# 查询神经网络
def query(self, input_list):
# convert inputs list to 2d array
# 将输入数组转换为 784*1 矩阵
inputs = numpy.array(input_list, ndmin=2).T
# calculate signals into hidden layer
# 计算隐藏层的输入信号
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
# 计算隐藏层的输出信号
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
# 计算输出层的输入信号
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final opuput layer
# 使用激活函数,计算出输出层的输出信号
final_outputs = self.activation_function(final_inputs)
return final_outputs
pass
pass
# number of input, hidden and output nodes
# 输入结点的数量
inodes = 784
# 隐藏结点的数量
hnodes = 300
# 输出结点的数量
onodes = 10
# learning rate is 0.3
# 学习率为 0.3
learning_rate = 0.3
# create instance of neural network
# 创建神经网络实例
n = neuralNetork(inodes, hnodes, onodes, learning_rate)
# load the mnist training data CSV file into a list
# training_data_file = open('mnist_dataset/mnist_train_100.csv', 'r')
# 读取训练样本数据
training_data_file = open('mnist_dataset/mnist_train.csv', 'r')
training_data_list = training_data_file.readlines()
training_data_file.close()
# train the neural
# 训练神经网络
train_num = 1
# go through all records in the training data set
# 遍历所有的样本数据,并输入到神经网络中
# 每次执行一行数据
for record in training_data_list:
print("Train:",train_num)
# split the record by the ',' commas
# 分隔一行数据,以 , 分隔
all_values = record.split(',')
# scale and shift the inputs
# 将像素数据转换为 0.01 到 0.99 之间的数据,像素数据范围为 0~2255
inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
# create the target output values (all 0.01,except the desired label which is 0.99)
# 设置目标数组,标记所在的元素设置为 0.99,其它元素设置为 0.01
targets = numpy.zeros(onodes) + 0.01
targets[int(all_values[0])] = 0.99
# 调用训练函数
n.train(inputs, targets)
train_num += 1
pass
# load the mnist test data CSV file into a list
# test_data_file = open('mnist_dataset/mnist_test_10.csv', 'r')
# 读取测试样本数据
test_data_file = open('mnist_dataset/mnist_test.csv', 'r')
test_data_list = test_data_file.readlines()
test_data_file.close()
# test the neural network
# 测试神经网络正确性
# scorecard for how well the network performs, initially empty
# scorecard 为结果数组,元素为 0 或 1,每一个值代表一次测试结果
# 准确率为 1 的数目除以所有元素个数。
scorecard = []
test_num = 1
# go through all the records in the test data set
# 遍历所有的样本数据,并输入到神经网络中
# 每次执行一行数据
for record in test_data_list:
print("Test", test_num)
# split the record by the ',' commas
# 分隔一行数据,以 , 分隔
all_values = record.split(',')
# correct answer is first value
# 每行的第一个值为准确的结果,读取准确的结果
correct_label = int(all_values[0])
# print(correct_label, "correct label")
# scale and shift the inputs
# 将像素数据转换为 0.01 到 0.99 之间的数据,像素数据范围为 0~2255
inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
# query the network
# 查询结果,得到输出结果
outputs = n.query(inputs)
test_num += 1
# the index of the highest value corresponds to the label
# 值最大的元素下标即为识别的数字
label = numpy.argmax(outputs)
# print(label, "network's answer")
# append correct or incorrect to list
# 判断得到的结果与标记的结果是否相等,并统计其准确率
if (label == correct_label):
# network's answer matches correct answer, add 1 to scorecard
scorecard.append(1)
else:
# network's answer doesn't match correct answer, add 0 to scorecard
scorecard.append(0)
pass
pass
# print(scorecard)
# calculate the performance score, the fraction of correct answers
# 计算准确率并输出
scorecard_array = numpy.asanyarray(scorecard)
print("performance = ", scorecard_array.sum() / scorecard_array.size)
输出结果
执行程序之后,准确率在 95% 以上。至此,一个简单的神经网络算法便完成了。
Github 代码库:https://github.com/noahsarkzhang-ts/first-neural-network
参考: